「数据结构学习笔记」#2 可持久化线段树
可持久化线段树
思想
可持久化线段树的思想如下
- 建立多棵线段树,代表不同版本。
- 为了降低空间复杂度,每棵线段树只储存与上一棵不同的部分,结构并不完整。换句话说,每个节点都是先继承上个版本,如果自己的儿子信息被修改了,那么新建立一个节点代替自己。而对于根节点,无论修改是否改变了根节点的信息,根节点的版本都改变了,因此必须新建节点,同时也能代表版本。
- 任意两棵线段树都能相减得到一棵新线段树,利用这颗线段树的信息解决问题。
多棵线段树,可以是 \(i \in [1,n]\),在每个 \([1,i]\) 上建树,这样相减能得到 \([l,r]\) 的线段树。也可以是每个「时间」的线段树,得到每段时间 \([s,t]\) 的信息。
无论是上述哪一种方式,都可以发现相邻两个版本间的差距只有一次修改。
如果是单点修改的话,那么两棵树的差别就是一条长度为 \(O(\log_2 n)\) 的链。被修改了的节点会单独创建,否则就直接继承先前版本。
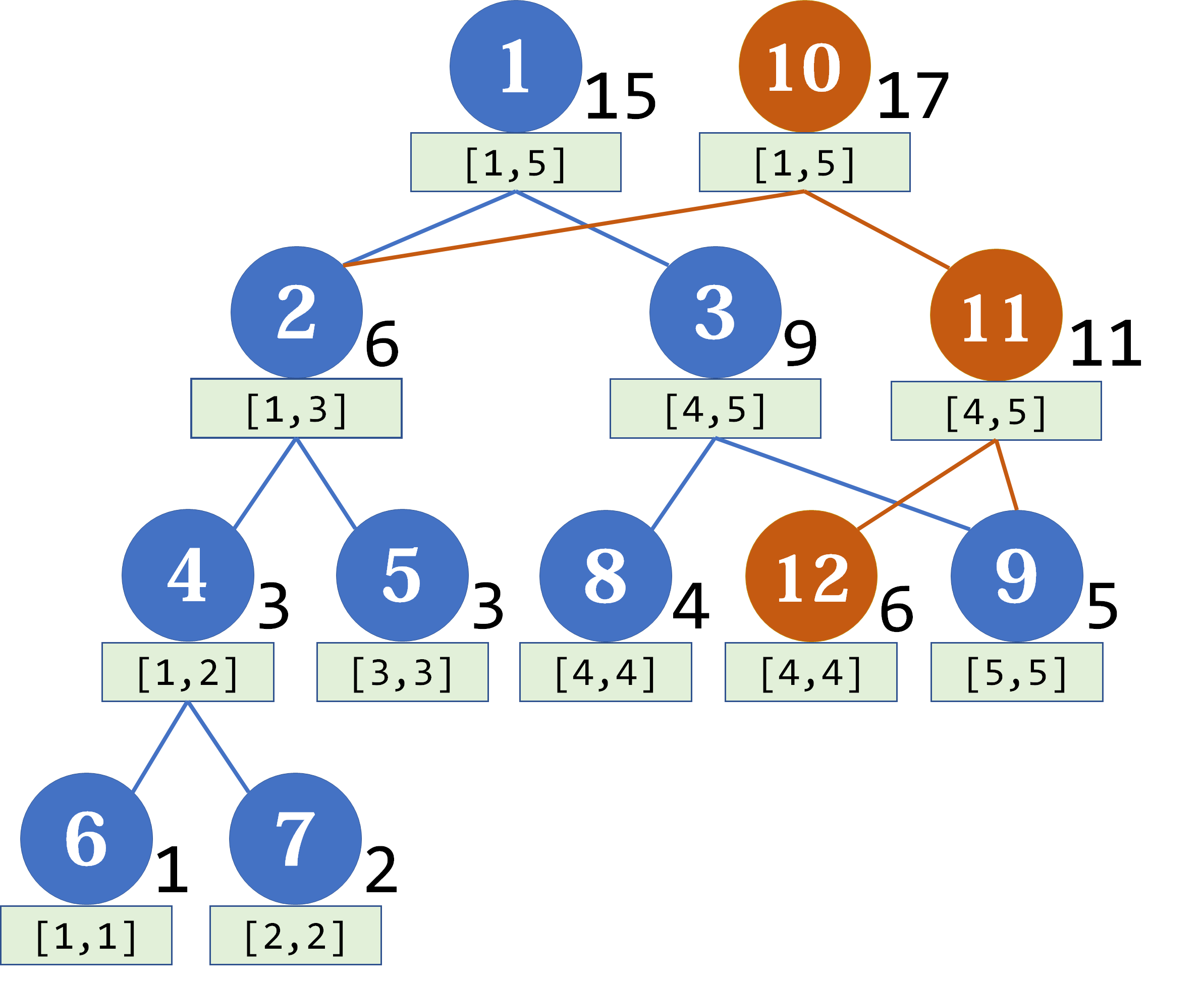
如图,蓝色的是前连续多少个版本的并集,而橙色是将节点 \(4\) 加上 \(2\) 的下一个版本。
区间修改呢?可以证明普通线段树区间操作每层节点最多访问 \(4\) 个,所以会访问的节点数量是 \(O(\log_2 n)\) 的。但是如果要下传标记呢?在一棵不完整的线段树上下传标记,如果暴力创建左右儿子那么空间就会爆炸,所以只能用标记永久化。
可以发现,如果没有初始树,那么每次操作要开大小为 \(O(\log_2 n)\) 的一棵树,总空间复杂度为 \(O(m \log_2 n)\),有初始树的话要加上 \(O(n \log_2 n)\)。
而修改操作则与普通线段树相同。
Code
建初始树
void build(int x,int l=1,int r=n) {
if(l==r) {
// init a node.
return;
}
int mid=(l+r)>>1;
build(ls[x],l,mid);
build(rs[x],mid+1,r);
pushup(x);
}
signed main() {
root[0]=++cnt;
build(root[0]);
}单点修改
void modify(int p,int q,int x,int d,int l=1,int r=n) {
// p是当前线段树,q是上一棵
if(l==r) {
// modify node p;
return;
}
ls[p]=ls[q], rs[p]=rs[q];
int mid=(l+r)>>1;
if(x<=mid) ls[p]=++cnt, modify(ls[p],ls[q],x,d,l,mid);
// 要修改的点在左边,那么ls[p]必然和ls[q]不同,所以新建。右边同理。
else rs[p]=++cnt, modify(rs[p],rs[q],x,d,mid+1,r);
pushup(p);
}
signed main() {
int x=read(), d=read();
if(root[i]==0) root[i]=++cnt;
modify(root[i],root[i-1],x,d);
}区间查
int query(int L,int R,int x,int l=1,int r=n) {
if(L<=l&&r<=R) return t[x];
int mid=(l+r)>>1;
int ans=0;
if(L<=mid) ans+=query(L,R,ls[x],l,mid);
if(R>mid) ans+=query(L,R,rs[x],mid+1,r);
return ans;
}(权值线段树)二分第 \(k\) 大。
int query(int p,int q,int k,int l=1,int r=n) {
if(l==r) return l;
int d=t[ls[p]]-t[ls[q]];
int mid=(l+r)>>1;
if(d>=k) return query(ls[p],ls[q],k,l,mid);
else return query(rs[p],rs[q],k-d,mid+1,r);
}考虑区间加法操作,我们只修改完全覆盖的区间的标记,不能完全覆盖则创建新节点,感性理解一下,时间和空间复杂度都是 \(O(\log_2 n)\),前文说到线段树区间操作最多访问一层中的 \(4\) 个节点,而不能被完全覆盖的最多只有两个。
void modify1(int L,int R,int d,int p,int q,int l=1,int r=n) {
ls[p]=ls[q], rs[p]=rs[q], sum[p]=sum[q], tag[p]=tag[q];
// 先继承
if(L<=l&&r<=R) { tag[p]+=d, sum[p]+=(r-l+1)*d; return; }
// 被完全覆盖,直接在继承的基础上修改
int mid=(l+r)>>1;
// 否则就要创建新节点
if(L<=mid) ls[p]=++cnt, modify1(L,R,d,ls[p],ls[q],l,mid);
if(R>mid) rs[p]=++cnt, modify1(L,R,d,rs[p],rs[q],mid+1,r);
pushup(p);
}
signed main() {
int l=read(), r=read(), d=read();
if(!root[i]) root[i]=++cnt;
modify1(l,r,root[i],root[i-1]);
}区间查就要记录当前区间的标记来保证正确性,同时要注意标记可能会溢出。
int query1(int L,int R,int x,int l=1,int r=n) {
if(L<=l&&r<=R) return sum[x]+(r-l+1)*tag[x];
int mid=(l+r)>>1, ans=(min(R,r)-max(L,l)+1)*tag[x];
if(L<=mid) ans+=query1(L,R,ls[x],l,mid);
if(R>mid) ans+=query1(L,R,rs[x],mid+1,r);
return ans;
}关于这玩意的空间,为了保险起见可以开 \(2^5 n\)
静态区间 kth
在每个 \(i\in[1,n]\),\([1,i]\) 上建立可持久化的权值线段树。第 \(r\) 棵线段树减去第 \(l\) 棵线段树就是 \([l,r]\) 的线段树。
然后在全局二分第 \(k\) 大即可,很好写。
参考
《算法竞赛》 By 罗勇军,郭卫斌
《算法竞赛进阶指南》 By 李煜东