字符串简单题目 1
luogu4391 无线传输
分析
题目说的很别扭,实际上是求一个最短的 \(S\) 的子串,满足这个子串自我拼接之后,\(S\) 是这个拼接串的子串。也就是 \(S\) 的最小周期。
若 \(|S|=n\),则答案为 \(n-next_n\)。证明如下:
如下图表示 \(S\) 的最大 Border 相交的情况,黑色部分是字符串 \(S\),蓝色部分是和红色部分是 \(next_n\),绿色部分 \(T=S[1,n-next_n]\)。
显然 \(T\) 是 \(S[1,next_n]\) 的一个前缀,又因为 \(S[1,next_n] = S[n-next_n+1,n]\),所以 \(T\) 后面又能再拼接上一块 \(T\)。而前面的黄色部分 \(S[n-next_n+1,next_n]\) 是前缀 Border 的最后 $next_n - (n-next_n+1) + 1 = 2 next_n - n $ 个字符,后面的黄色部分是后缀 Border 的最后 \(n - 2(n-next_n) = 2next_n - n\) 个字符,所以黄色这这两块是等价的。由于左边的黄色部分是 \(T\) 的一个前缀,所有右边的黄色部分也是 \(T\) 的前缀,于是在第二个 \(T\) 后面再接一个 \(T\),此时 \(S\) 必然为它的子串。
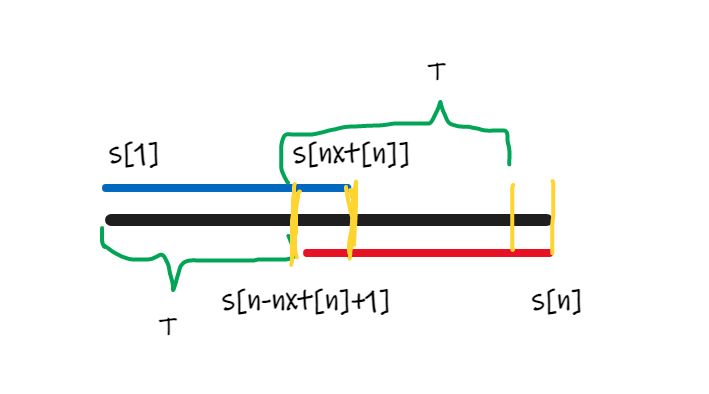
那么最大 Border 不重叠呢?看下图,颜色所代表的信息与上图相同。不难发现红色部分就是等价于蓝色部分,蓝色部分是 \(T\) 的前缀。所以再接一个 \(T\) 就能覆盖整个串了。

综上,\(n-next_n\) 一定是 \(S\) 的一个周期。
而 \(next_n\) 是 \(S\) 的最大 Border,对应的 \(n-next_n\) 就是 \(S\) 的最小周期。
luogu3435 Periods of Words
上题证明了,\(n-next_n\) 是 \(S\) 的最小周期,同理 \(i-next_i\) 是前缀 \(S[1,i]\) 的最小周期。由于 \(next_{next_i}\) 是 \(S[1,i]\) 的次小 Border,所以只要对于一个前缀 \(S[1,i]\),只要找到最小的非 \(0\) border \(t\),最大周期即为 \(i-t\)。方法是令 \(t=i\),如果 \(next_t > 0\),那么就不断让 \(t=next_t\)。这个过程也是可以记忆化的。
luogu4824 Censoring
套路性的维护一个栈,然后如果匹配到一个 \(T\) 串,那么那么就让栈顶减小 \(|T|\) 即可。最后留在栈里的即为答案。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+5;
int n, m, top, nxt[N], f[N], stk[N];
char a[N], b[N];
void pre() {
nxt[1]=0;
for(int i=2,j=0;i<=n;++i) {
while(j&&a[i]!=a[j+1]) j=nxt[j];
j+=a[i]==a[j+1];
nxt[i]=j;
}
}
signed main() {
scanf("%s%s",b+1,a+1);
n=strlen(a+1), m=strlen(b+1);
pre();
for(int i=1,j=0;i<=m;++i) {
while(j&&b[i]!=a[j+1]) j=nxt[j];
j+=b[i]==a[j+1];
f[i]=j;
stk[++top]=i;
if(f[i]==n) top-=n, j=f[stk[top]];
}
for(int i=1;i<=top;++i) printf("%c",b[stk[i]]);
puts("");
}
luogu2375 动物园
要求前缀和后缀不重叠还要计数。
设 \(f_i\) 表示 \(S[1,i]\) 的 Border 的个数,也就是如果 \(next_i = j\),那么有 \(f_i = f_j +1\)。
对于每一个 \(i\),找到最大的满足 \(i \ge 2j\) 的 Border \(j\),此时 \(num_i = f_j\)。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=1e6+5, mod=1e9+7;
int t, n, ans, nxt[N], f[N];
char s[N];
int read() {
int a=0, f=1; char c=getchar();
while(!isdigit(c)) {
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a*f;
}
void pre() {
nxt[1]=0, f[1]=1;
for(int i=2,j=0;i<=n;++i) {
while(j&&s[i]!=s[j+1]) j=nxt[j];
if(s[i]==s[j+1]) ++j;
nxt[i]=j;
f[i]=f[j]+1;
}
}
void solve() {
ans=1;
scanf("%s",s+1), n=strlen(s+1);
pre();
for(int i=2,j=0;i<=n;++i) {
while(j&&s[i]!=s[j+1]) j=nxt[j];
if(s[i]==s[j+1]) ++j;
while(i<2*j) j=nxt[j];
(ans*=f[j]+1)%=mod;
}
printf("%lld\n",ans);
}
signed main() {
t=read();
while(t--) solve();
}
luogu3426 Template
首先印章上的字符串一定是原串的一个 Border,但是原串的 Border 不一定合法。
而如果一个 Border 合法,那么所有 Border 为它的下标之间的间隔绝对小于它的长度。这样就可以完成整个串的覆盖。观察样例就能得到这两个结论。
所以答案就要从原串 \(S\) 的 Border 里面选择,优先考虑最小的。
设 \(ans_i\) 为候选答案中第 \(i\) 小的答案。考虑 \(ans_{i-1}\) 不合法,但是 \(ans_i\) 合法的情况。
由于 \(ans_{i-1}\) 不合法,所以要排除所有 Border 为 \(ans_{i-1}\) 且不为 \(ans_i\) 的下标(\(ans_{i-1}\) 一定是 \(ans_i\) 的 Border)。排除之后,又要再次统计 Border 为 \(ans_i\) 的下标的间隔。可以用链表来实现快速查询和删除。
如何快速实现排除下标呢?引入一种数据结构,名为——失配树。也叫 \(fail\) 树和 \(next\) 树。简而言之,就是把 \(next_i\) 向 \(i\) 连一条边。
它的主要性质是:点 \(x\) 如果是点 \(y\) 的祖先,那么 \(S[1,x]\) 是 \(S[1,y]\) 的一个 Border。如果 \(x\) 和 \(y\) 之间没有祖孙关系,那么绝不满足上述性质。
也就是说,删去所有 Border 为 \(ans_{i-1}\) 且 Border 不为 \(ans_i\) 的下标,只要在失配树中删去 \(ans_{i-1}\) 子树内所有非 \(ans_i\) 的节点即可。
从小到大枚举答案,如果某个 \(ans_i\) 满足了,答案就是 \(ans_i\)。
参考:[POI2005][luogu3462] SZA-Template [fail树]
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+5;
int n, m, gap, rec, fail[N], pre[N], suf[N], ans[N];
int tot, h[N], to[N], nxt[N];
char s[N];
void add(int x,int y) {
to[++tot]=y, nxt[tot]=h[x], h[x]=tot;
}
void prepre() {
fail[1]=0;
for(int i=2,j=0;i<=n;++i) {
while(j&&s[i]!=s[j+1]) j=fail[j];
if(s[i]==s[j+1]) ++j;
fail[i]=j;
}
for(int i=1;i<=n;++i) add(fail[i],i);
// 每一个点都要加入失配树
for(int i=n;i;i=fail[i]) ans[++m]=i;
// 这里是从大到小存的
// for(int i=1;i<=m;++i) printf("%lld\n",ans[i]);
for(int i=1;i<=n;++i) pre[i]=i-1, suf[i]=i+1;
}
void del(int x) {
suf[pre[x]]=suf[x], pre[suf[x]]=pre[x];
gap=max(gap,suf[x]-pre[x]);
pre[x]=suf[x]=0;
}
void dfs(int x,int zero) {
del(x);
for(int i=h[x];i;i=nxt[i]) {
int y=to[i];
if(y==zero) continue;
del(y);
dfs(y,zero);
}
}
signed main() {
scanf("%s",s+1);
n=strlen(s+1);
prepre();
for(int i=m;i;--i) {
dfs(ans[i+1],ans[i]);
// 这个可以模拟一下,注意第一次先删去了所有根节点0所有Border不是ans[m]的节点
if(gap<=ans[i]) { rec=ans[i]; break; }
}
printf("%lld\n",rec);
}
CF126B Password
既是前缀,又是后缀,又在中间出现过。
不难想到,既是前缀又是后缀,说明一定是 \(S\) 的一个 Border,所以答案最大为 \(next_n\)。在中间也出现过,假设出现的位置是 \(i_0\),那么答案也是 \(S[1,i_0]\) 的一个 Border。因此只要从大到小寻找满足
- 是 \(S\) 的 Border。
- 存在至少一个 \(i \in [1,n-1]\),满足 \(next_j = i\),
的最大的 \(j\) 即可。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n, nxt[N], v[N];
char s[N];
int main() {
scanf("%s",s+1);
n=strlen(s+1);
for(int i=2,j=0;i<=n;++i) {
while(j&&s[i]!=s[j+1]) j=nxt[j];
if(s[i]==s[j+1]) ++j;
nxt[i]=j;
if(i!=n) v[j]=1;
}
int ans=nxt[n], fg=0;
while(ans) {
if(v[ans]) { fg=1; break; }
ans=nxt[ans];
}
if(!fg) { puts("Just a legend"); return 0; }
for(int i=1;i<=ans;++i) printf("%c",s[i]);
puts("");
}CF858D Polycarp's phone book
对于每个字符串 \(S_i\),找到一个最短的子串,满足这个子串是且只是 \(S_i\) 的子串。
一个想法把所有字符串的所有子串插入集合,对于每个字符串 \(S_i\),从小到大枚举所有子串,在不考虑 \(S_i\) 的所有子串的情况下查看是否存在这个子串。
这个显然是不行的,考虑优化。注意到,只要把所有后缀都插入集合,枚举的时候只枚举起点,就能找到所有 \(S_i\) 的子串。
既然是和字符串相关,那么这个集合可以用 Trie 来在一个比较优的复杂度内实现。
考虑什么时候可行。设 \(cnt_x\) 表示字符 \(x\) 在集合中的出现次数,如果 \(S_i\) 的某个子串的结尾字符的 \(cnt\) 为 \(0\),由于之前已经删掉了 \(S_i\) 的所有后缀,所以此时这个子串一定是唯一的,输出即可。然后再把所有后缀插入回去。
#include<bits/stdc++.h>
using namespace std;
const int N=2e6+5;
int n, tot, d, cnt[N], trie[N][15];
char a[N][15], ans[15], t[15];
int read() {
int a=0, f=1; char c=getchar();
while(!isdigit(c)) {
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a*f;
}
void insert(char* s) {
int x=0, len=strlen(s);
for(int i=0;i<len;++i) {
int a=s[i]-'0';
if(!trie[x][a]) trie[x][a]=++tot;
x=trie[x][a], ++cnt[x];
}
}
void del(char* s) {
int x=0, len=strlen(s);
for(int i=0;i<len;++i) {
int a=s[i]-'0';
x=trie[x][a], --cnt[x];
}
}
void find(char* s) {
int x=0, len=strlen(s);
for(int i=0;i<len;++i) {
t[i]=s[i];
int a=s[i]-'0';
x=trie[x][a];
if(cnt[x]==0) {
if(i+1<d) {
d=i+1;
//此时答案长度为i+1
t[i+1]='\0';
// 截取t[0,i]这一段,因为puts()遇到'\0'会停止
strcpy(ans,t);
break;
}
}
}
}
int main() {
n=read();
for(int i=1;i<=n;++i) {
scanf("%s",a[i]);
for(int j=0;j<9;++j) insert(a[i]+j);
}
for(int i=1;i<=n;++i) {
d=10;
for(int j=0;j<9;++j) del(a[i]+j);
for(int j=0;j<9;++j) find(a[i]+j);
for(int j=0;j<9;++j) insert(a[i]+j);
puts(ans);
}
}