「图论学习笔记」#4 二分图相关
二分图最小点覆盖
给定一张二分图,求出一个最小的点集 \(S\),使得图中任意一条边都至少有一个端点在 \(S\) 中。这个问题称为二分图的最小点覆盖,简称最小覆盖。
\(\text{k\"onig}\) 定理
二分图最小覆盖包含的点数等于此图最大匹配包含的边数。
看证明过程时,请牢记增广路,最大匹配,匹配点,匹配边的定义,不然像我这种不太聪明的可能会多想很多没用的东西。
证明:
二分图的最大匹配是所有此图边的子集,且其中的边两两没有共同端点。那么最小覆盖中必然包含最大匹配中每一条边的任意一个端点,不然存在一条最大匹配中的边满足任意一个端点都不在其中。也就是最小覆盖包含的点数大于等于最大匹配包含的边数。
如下进行构造。
- 求出二分图最大匹配。
- 从左部每一个非匹配点进行 DFS 寻找增广路,必定失败,同时标记访问过的点。
- 取左部未被标记的点、右部被标记的点。得到最小覆盖。
以下证明它的正确性。由于出发点是左部非匹配点,那么左部匹配点一定没有被标记。而右部被标记的一定是匹配点,否则就找到了一条增广路,与已经求出最大匹配相矛盾。这样选出的点数恰好是最大匹配的边数。
以下证明它能够覆盖所有的边。分类讨论。
- 连接两个匹配点的边,只会有一个端点被选择,即被覆盖。这是因为求出最大匹配的 DFS 中匹配点与非匹配点必然是交替访问的,而由于左边选没有标记的,右边选有标记的,所以绝对不会出现下图中选择 \(1\) 与 \(A\) 的情况。进一步知道,对于一条匹配边,它的两个端点必然只选其中一个。
- 连接两个非匹配点的边。求出最大匹配后便不存在了,不然就是一条增广路。
- 连接左部非匹配点 \(u\),右部匹配点 \(v\)。\((u \rightarrow v)\) 一定被访问,\(u\) 一定不被选中,\(v\) 一定被选中,被覆盖。
- 连接左部匹配点 \(u\),右部非匹配点 \(v\)。如果 \(u\) 被访问了,那么沿着 \((u \rightarrow v)\) 一定能找到一条增广路,矛盾。所以 \(u\) 一定不被访问,进而二者没有被标记。那么就一定选择 \(u\),一定不选择 \(v\),被覆盖。
图片侵删。
红色边为最大匹配,红色点为最小覆盖。
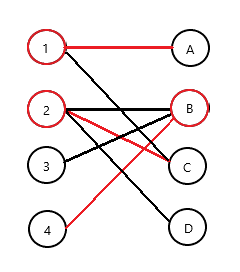
二分图最大独立集
一般图情况
给定一张无向图,求出一个点集,满足任意两点之间没有边相连,称之为这张图的一个独立集。包含点最多的那个称为最大独立集。
给定一张无向图,求出一个点集,满足任意两点之间都有一条边相连,称之为这张图的一个团。包含点最多的那个称为最大团。
一个定理:对于无向图 \(G\),其最大团为其补图 \(G'\) 的最大独立集。
\(G=(V,E)\) 的补图 \(G'=(V,E')\),其中 \(E' = \{(x,y) \notin E \}\)。也就是对于 \(x,y \in V\),如果它们两个点 \(G\) 中没有边,那么在 \(G'\) 中就有边,反之没有边。也可以理解为,将 \(G\) 扩展成一个完全图,然后减掉原有的边。
很重要的补图转化思想,从问题的另一面打开突破口。
对于一般图,最大团与最大独立集是 NPC 问题。(好了不用学了)
二分图情况
一个定理:
设 \(G\) 为有 \(n\) 个节点的二分图,\(G\) 的最大独立集为 \(n\) 减去最大匹配的边数(最小覆盖的点数)。
证明:
选出最多的点构成独立集。等于在图中去掉最少的点,使得剩下的点两两不相连。也就是用最少的点去覆盖所有的边(然后把它们删了)。
DAG 的最小路径点覆盖
给定一个 DAG,要求用尽量少的不相交的简单路径,恰好覆盖 DAG 的所有点,这个问题成为 DAG 的最小路径点覆盖问题。
设原来的 DAG 为 \(G = (V,E)\),共有 \(n\) 个节点。对于 \(x \in V\),把它拆成 \(x\) 与 \(x+n\) 两个点。将 \([1,n]\) 作为左部点,\([n+1,2n]\) 作为右部点建立二分图。对于原图中的边 \((x \rightarrow y)\),再二分图中连 \((x \rightarrow y+n)\)。最终得到的二分图 \(G'\) 称为 \(G\) 的拆点二分图。
定理:
\(G\) 的最小路径点覆盖包含的路径条数等于 \(n\) 减去 \(G'\) 的最大匹配数。
证明暂略,有时间补上。
如果简单路径可相交,那么就是 DAG 的最小路径可重复点覆盖问题。
最小路径可重复点覆盖中,如果有两条路径 \((x \rightarrow p \rightarrow y)\),\((u \rightarrow p \rightarrow v)\),那么这两条路径是相交的。但是如果添加一条边 \((x \rightarrow y)\),那么就能让他们不相交了。
进一步地,对于任意能够间接连通两个点,都添加一条边让它们直接连通,然后c拆点跑最大匹配,用 \(n\) 减去就行了。但是一旦加边后,这就不再是一个 DAG 了,所以如果要用网络流算法求最大匹配的话,对于间接连通的点对 \((x,y)\),只需要添加 \((x \rightarrow y+n)\)。但如果是匈牙利算法的话就不用考虑,因为邻接矩阵的特殊结构。
上述判断间接连通可以用 Floyd 传递闭包实现。