最小树型图

最小树形图，也可以理解为有向图的最小生成树。

更学术地说，在一张有向带权图 \(G\) 中，找出一棵以 \(root\) 为根，权值和最小的有向生成树，满足：

• \(root\) 入度为 0，其余节入度为 1
• 任意两点 \((u,v)\) 间，有且仅有 1 条简单路径

朱刘算法

理论

朱刘算法是一个能在 \(O(nm)\) 的时间内验证有向带权图是否有最小树型图，并且能求出此图。

首先保证图没有自环且连通。

接着就是算法的过程：

1. 对于每一个点，分别找到它们的最小入边，构成一张新图。
2. 如果新图没有环且连通，那么此时就是所求的最小树形图。
3. 否则将一个环缩成一个点，建立新图，重新计算边权，重复以上过程。

严格证明？不会。

但也是类似于 Kruskal 的贪心，只是多了缩点。

感性理解一下，显然是对的。

实现

如何去实现呢？前两步显然不难，最大的问题在于缩点后的边权怎么计算。

对于一个环，最终一定是将它断成一条链，那么就必须舍弃一条边。贪心删除最大的边？显然不可以，如果向下图一样删边，那么如果 A 只有一条权值巨大的入边呢？这个贪心就 fAKe 了。

断环为链

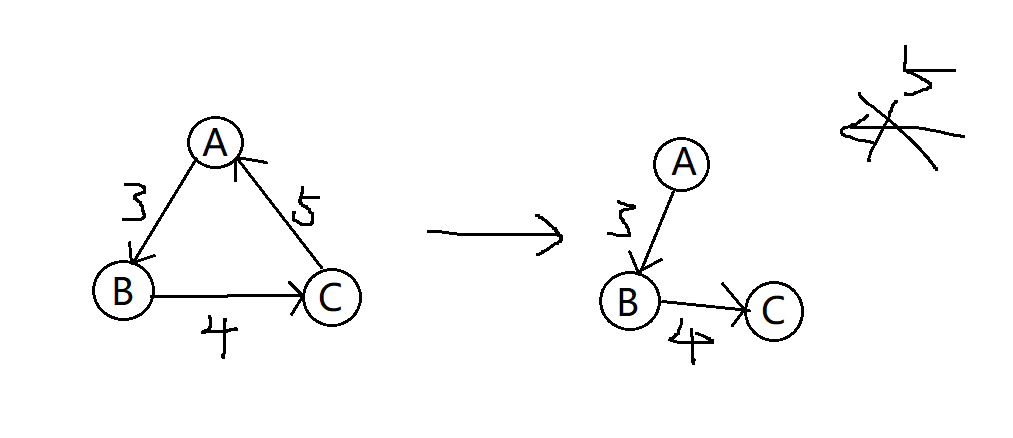
所以我们不能直接破坏这个环。

将环缩成一个点 \(u\) 之后，\(u\) 继承了所有环内节点的所有环外入边。而建立新图后只会选择一条最小入边。且选择对于一个环内节点 \(v\)，选择 \(v\) 的环外入边只会被动地删掉 \(v\) 的环内入边。

所以如果我们先把环内所有边的权值统计入答案，再把每条环外入边的权值减去相对应的环内入边的权值，则无论选择那条环外入边，最终都不影响答案。

如下图，\((Y \rightarrow B)\) 早在第一个阶段就被 pass 掉。\((X \rightarrow B)\) 是 \(B\) 的一条环外入边，那么如果把 \(X\) 的权值 \(x\) 减去 \(B\) 的环内入边的权值 \(3\)，即直接累加 \(x-3\) 的话，就相当于删去了 \((A \rightarrow B)\) 这条边。且对于其他的环外入边，这种方案都是可行的。

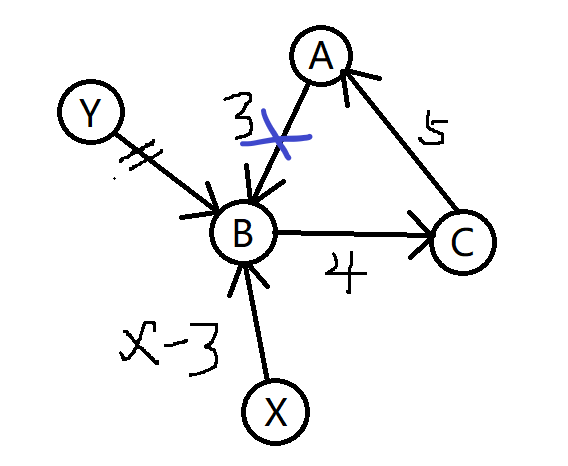
于是这个问题就解决了，具体看代码。

int n, m, root, in[N], pre[N], v[N], id[N];
struct edge { int u, v, w; } e[M];
inline int zhuliu() {
	int ans=0;
	while(1) {
        int cnt=0; // 环的数量
		memset(in,0x3f,sizeof(in));
        // in[x]=x的最小入边边权, pre[x]=in[x]对应的点
		memset(v,0,sizeof(v));
        // v[x]=在新图中，能从哪一个点访问到x
		memset(id,0,sizeof(id));
        // 标记所属的环（或者点）
		for(int i=1;i<=m;++i) if(e[i].u!=e[i].v&&e[i].w<in[e[i].v])
			in[e[i].v]=e[i].w, pre[e[i].v]=e[i].u;
        // 寻找最小边权
		for(int i=1;i<=n;++i) if(in[i]==inf&&i!=r) return -1;
        // 不连通，不存在最小树型图
		in[root]=0;
        // 根没有入边
		for(int i=1;i<=n;++i) {
			ans+=in[i];
            // 直接累计边权
			int x=i;
			while(v[x]!=i&&!id[x]&&x!=root) v[x]=i, x=pre[x];
            // 标记能够访问到的点，如果访问回来了，那么就找到环了
			if(x!=root&&!id[x]) {
				id[x]=++cnt;
				for(int y=pre[x];y!=x;y=pre[y]) id[y]=cnt;
                // 所有换上节点标记为第几个环
			}
		}
		if(!cnt) break;
        // 没有环，直接结束
		for(int i=1;i<=n;++i) if(!id[i]) id[i]=++cnt;
        // 不在环中的点，自成一个“环”，便于统计
		for(int i=1;i<=m;++i) {
			int u=e[i].u, v=e[i].v;
			e[i].u=id[e[i].u], e[i].v=id[e[i].v];
            // 缩点，将每条边的两个端点改为它们所属的环编号
			if(u!=v) e[i].w-=in[v];
            // 不是自环，进行减权操作
		}
		n=cnt, root=id[root];
        // 修改信息
	}
	return ans; // 返回答案
}

题目

UVA11865 Stream My Contest

二分答案。

二分最小带宽 \(mid\)，判断是否能用带宽不小于 \(mid\) 的边构成一棵花费不超过 \(cost\) 的最小树型图。

#include<bits/stdc++.h>
using namespace std;
#define ll long long 
const int N=100, M=10005, inf=0x3f3f3f3f;
int T, n, m, len, tot, cost, root, in[N], pre[N], v[N], id[N];
struct edge { int u, v, w, b; } t[M], e[M];
inline ll zhuliu(int n,int m) {
	ll ans=0;
	while(1) {
		for(int i=1;i<=n;++i) in[i]=inf;
		for(int i=1;i<=m;++i) if(e[i].u!=e[i].v&&e[i].w<in[e[i].v])
			in[e[i].v]=e[i].w, pre[e[i].v]=e[i].u;
		for(int i=1;i<=n;++i) if(in[i]==inf&&i!=root) return -1;
		int cnt=0;
		memset(v,0,sizeof(v));
		memset(id,0,sizeof(id));
		in[root]=0;
		for(int i=1;i<=n;++i) {
			ans+=in[i];
			if(ans>cost) return -1;
			int x=i;
			while(v[x]!=i&&!id[x]&&x!=root) v[x]=i, x=pre[x];
			if(x!=root&&!id[x]) {
				id[x]=++cnt;
				for(int y=pre[x];y!=x;y=pre[y]) id[y]=cnt;
			}
		}
		if(!cnt) break;
		for(int i=1;i<=n;++i) if(!id[i]) id[i]=++cnt;
		for(int i=1;i<=m;++i) {
			int u=e[i].u, v=e[i].v;
			e[i].u=id[e[i].u], e[i].v=id[e[i].v];
			if(u!=v) e[i].w-=in[v];
		}
		n=cnt, root=id[root];
	}
	return ans;
}
inline bool check(int x) {
	tot=n, len=0, root=1;
	for(int i=1;i<=m;++i) if(t[i].b>=x) e[++len]=t[i];
	ll ans=zhuliu(tot,len);
	return ans<=cost&&ans!=-1;
}
inline void sol() {
	int l=inf, r=0, mid;
	scanf("%d%d%d",&n,&m,&cost);
	for(int i=1;i<=m;++i) {
		scanf("%d%d%d%d",&t[i].u,&t[i].v,&t[i].b,&t[i].w);
		++t[i].u, ++t[i].v;
		l=min(l,t[i].b), r=max(r,t[i].b);
	}
	if(!check(l)) { printf("streaming not possible.\n"); return; }
	while(l<r) {
		mid=(l+r+1)/2;
		if(check(mid)) l=mid; else r=mid-1;
	}
	printf("%d kbps\n",l);
}
int main() { for(scanf("%d",&T);T--;sol()); }

 

小店购物

如果把所有要买的物品都买一次，那么剩下的物品就都能用最小价格买了。所以目标就是计算所有物品都买一次的花费。

如果买 \(u\) 能把 \(v\) 优惠到花费 \(w\) 元，那么连一条 \((u \rightarrow v)\)，权值为 \(w\) 的边。同时将虚拟节点 \(n+1\) 与每个物品连一条权值为原价 \(c_i\) 的边。

虚拟节点目的是让图连通并符合题意，注意这里不能是 0，因为在朱刘算法中，多个数组的 0 是未计算的状态。

这里的 \(n\) 是要买的商品总数，连完边后就多了一个虚拟节点，\(n\) 要 变成 \(n+1\)。边数 \(m\) 就是要买的商品数与优惠的数量之和。

建完图后跑最小树型图，最后在加上剩下的物品就好了。

#include<bits/stdc++.h>
using namespace std;
const int N=60, inf=0x3f3f3f3f;
int n, m, root, mp[N], c[N], pre[N], id[N], v[N];
double ans, a[N], in[N];
struct edge { int u, v; double w; } e[N*N];
inline edge trans(int u,int v,double w) {
	edge e;
	e.u=u, e.v=v, e.w=w;
	return e;
}
inline double zhuliu() {
	while(1) {
		for(int i=1;i<=n;++i) in[i]=inf;
		for(int i=1;i<=m;++i) if(e[i].u!=e[i].v&&e[i].w<in[e[i].v])
			in[e[i].v]=e[i].w, pre[e[i].v]=e[i].u;
		for(int i=1;i<=n;++i) if(in[i]==inf&&i!=root) return -1;
		int cnt=0;
		memset(v,0,sizeof(v));
		memset(id,0,sizeof(id));
		in[root]=0;
		for(int i=1;i<n;++i) {
			ans+=in[i];
			int x=i;
			while(v[x]!=i&&!id[x]&&x!=root) v[x]=i, x=pre[x];
			if(x!=root&&!id[x]) {
				id[x]=++cnt;
				for(int y=pre[x];y!=x;y=pre[y]) id[y]=cnt;
			}
		}
		if(!cnt) break;
		for(int i=1;i<=n;++i) if(!id[i]) id[i]=++cnt;
		for(int i=1;i<=m;++i) {
			int u=e[i].u, v=e[i].v;
			e[i].u=id[e[i].u], e[i].v=id[e[i].v];
			if(u!=v) e[i].w-=in[v];
		}
		n=cnt, root=id[root];
	}
	return ans;
}
int main() {
	int t1, t2;
	scanf("%d",&t1);
	for(int i=1;i<=t1;++i) {
		double x; int y;
		scanf("%lf%d",&x,&y);
		if(y) mp[i]=++n, a[n]=x, c[n]=y;
	}
	scanf("%d",&t2);
	m=n+t2;
	for(int i=1;i<=n;++i) e[t2+i]=trans(n+1,i,a[i]);
	for(int i=1;i<=t2;++i) {
		int u, v; double w;
		scanf("%d%d%lf",&u,&v,&w);
		u=mp[u], v=mp[v];
		if(!u||!v) continue;
		a[v]=min(a[v],w);
		e[i]=trans(u,v,w);
	}
	++n, root=n;
	for(int i=1;i<=n;++i) ans+=a[i]*(c[i]? c[i]-1:0);
	printf("%.2lf\n",zhuliu());
}