「网络流 24 题」#1
网络流 24 题,很多都是与二分图相关,「能用网络流算法求解」的题目,所以下文叙述时会更多地讨论题目的本质。
只能说,24 题毕竟也仅仅是比板子要复杂一些,就将就着看个乐呵吧。
luogu2756 飞行员配对方案问题
分析
显然,将英国飞行员和外籍飞行员分别作为二分图的左右节点,一个英国飞行员只能和一个外籍飞行员配合,满足「每个集合内部有 \(0\) 条边」的 0 要素和「每个点最多与 \(1\) 条匹配边相连」的 1 要素。
派出最多的飞机,转化为求这张二分图的最大匹配。
至于输出方案,最大流算法结束后,有流经过的点和边就是匹配点、匹配边。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=105, inf=0x3f3f3f3f;
int n, m, s, t, maxflow, d[N], hh[N];
int tot=1, h[N], to[N*N], nxt[N*N], w[N*N];
void add(int x,int y,int z) {
to[++tot]=y, w[tot]=z, nxt[tot]=h[x], h[x]=tot;
}
int read() {
int a=0, f=1; char c=getchar();
while(!isdigit(c)) {
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a*f;
}
bool bfs() {
queue<int> q;
memset(d,0,sizeof(d));
d[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]||!z) continue;
d[y]=d[x]+1;
q.push(y);
if(y==t) return 1;
}
}
return 0;
}
int dinic(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]!=d[x]+1||!z) continue;
int k=dinic(y,min(res,z));
if(!k) d[y]=0;
else w[i]-=k, w[i^1]+=k, res-=k;
if(!res) return flow;
}
return flow-res;
}
int main() {
m=read(), n=read();
s=n+1, t=n+2;
while(1) {
int x=read(), y=read();
if(x!=-1&&y!=-1) add(x,y,1), add(y,x,0);
else break;
}
for(int i=1;i<=m;++i) add(s,i,1), add(i,s,0);
for(int i=m+1;i<=n;++i) add(i,t,1), add(t,i,0);
n+=2;
while(bfs()) maxflow+=dinic(s,n);
printf("%d\n",maxflow);
for(int x=1;x<=m;++x) for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(y==s||z) continue;
// 由于边容量为 1,所以z!=0绝对没有流经过
// 不能是到源点的边
printf("%d %d\n",x,y);
}
}luogu3254 圆桌问题
分析
将单位看作左部点,餐桌看作右部点,显然这是一张二分图。
考虑转化成二分图模型。同一个单位来的代表不能在同一个餐桌就餐,那么餐桌与代表之间两两有一条边。而单位 \(i\) 派出 \(r_i\) 个代表,说明它最多与 \(r_i\) 条匹配边相连,第 \(j\) 个餐桌能容纳 \(c_j\) 个代表,说明它最多和 \(c_j\) 条匹配边相连。二分图多重匹配板子。
解决这个问题,只需要将源点到左部点 \(i\) 的容量设置成 \(r_i\),右部点 \(j\) 到汇点的容量设置成 \(c_j\),跑最大流即可。求出多重匹配后,如果匹配书不等于人数,那么无解。
输出方案时记得将编号搞到 \([1,n]\) 之间。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=500, inf=0x3f3f3f3f;
int n, m, s, t, sum, maxflow, d[N], hh[N];
int tot=1, h[N], to[N*N], nxt[N*N], w[N*N];
void add(int x,int y,int z) {
to[++tot]=y, w[tot]=z, nxt[tot]=h[x], h[x]=tot;
}
int read() {
int a=0, f=1; char c=getchar();
while(!isdigit(c)) {
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a*f;
}
bool bfs() {
queue<int> q;
memset(d,0,sizeof(d));
d[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]||!z) continue;
d[y]=d[x]+1;
q.push(y);
if(y==t) return 1;
}
}
return 0;
}
int dinic(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]!=d[x]+1||!z) continue;
int k=dinic(y,min(res,z));
if(!k) d[y]=0;
else w[i]-=k, w[i^1]+=k, res-=k;
if(!res) return flow;
}
return flow-res;
}
int main() {
m=read(), n=read();
s=n+m+1, t=n+m+2;
for(int i=1;i<=m;++i) {
int x=read();
add(s,i,x), add(i,s,0);
sum+=x;
}
for(int i=1;i<=n;++i) {
int x=read();
add(i+m,t,x), add(t,i+m,0);
}
for(int i=1;i<=m;++i) for(int j=1+m;j<=n+m;++j)
add(i,j,1), add(j,i,0);
while(bfs()) maxflow+=dinic(s,inf);
if(maxflow!=sum) { puts("0"); return 0; }
puts("1");
for(int x=1;x<=m;++x) {
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(y!=s&&!z) printf("%d ",y-m);
}
puts("");
}
}luogu2763 试题库问题
分析
类型作为左部点,题目作为右部点。
要选出 \(c_i\) 道类型的题,就是 \(i\) 最多与 \(c_i\) 条匹配边相连。
如果第 \(j\) 道题可以属于 \(p\) 类,对应的点之间连容量为 \(1\) 的边。
对于每道题 \(j\),它最多与 \(1\) 条匹配边相连。
仍然是多重给匹配,除了建模,其他与上题完全相同。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5, inf=0x3f3f3f3f;
int n, k, m, s, t, cnt[N], d[N];
int tot=1, h[N], hh[N], to[N*N], nxt[N*N], w[N*N];
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
void add(int x,int y,int z) {
to[++tot]=y, w[tot]=z, nxt[tot]=h[x], h[x]=tot;
}
bool bfs() {
queue<int> q;
memset(d,0,sizeof(d));
d[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]||!z) continue;
d[y]=d[x]+1;
q.push(y);
if(y==t) return 1;
}
}
return 0;
}
int dfs(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]!=d[x]+1||!z) continue;
int k=dfs(y,min(res,z));
if(!k) d[y]=0; else w[i]-=k, w[i^1]+=k, res-=k;
if(!res) return flow;
}
return flow-res;
}
int dinic() {
int maxflow=0;
while(bfs()) maxflow+=dfs(s,inf);
return maxflow;
}
int main() {
k=read(), n=read();
s=0, t=n+k+1;
for(int i=1;i<=k;++i) {
m+=cnt[i]=read();
add(s,i,cnt[i]), add(i,s,0);
}
for(int i=1;i<=n;++i) {
int num=read();
while(num--) {
int x=read();
add(x,i+k,1), add(i+k,x,0);
}
}
for(int i=1;i<=n;++i) add(i+k,t,1), add(t,i+k,0);
int ans=dinic();
if(ans!=m) { puts("No Solution!"); return 0; }
for(int x=1;x<=k;++x) {
printf("%d: ",x);
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(y==s||z) continue;
printf("%d ",y-k);
}
puts("");
}
}luogu2764 最小路径覆盖问题
DAG 最小路径覆盖板子题,具体做法不再赘述,看代码就能懂。
更大的问题是输出方案。由于在拆点二分图上,路径必定是一个左部点和右部点交替出现。设 \(p(x)=y-n\) 为在最大流(的分层图)中与左部点 \(x\) 相连的右部点,\(q(y-n)=x\) 为与右部点 \(y\) 相连的左部点。方向都是 \((x \rightarrow y)\)。由于右部点是左部点拆过去的,平移了 \(n\) 位,所以要减去 \(n\)。
初始的时候,\(p(x)=q(x)=i\)。
对于一个 \(x\),如果 \(p(x)=x\) 且没有被标记,那么说明 \(x\) 是一条路径的尽头,直接从 \(x\) 往前递归输出即可。具体流程如下:
- \(x=0\),结束递归。
- \(x \neq 0\),如果 \(q(x) \neq x\),那么递归 \(q(x)\)。
- 递归结束后标记 \(x\),不再使用。
- 输出 \(x\),确保是按照顺序。
这么做的根据是,对于一张拆点二分图的最大匹配中,其匹配边 \((x,y+n)\) 对应了原图中的 \((x,y)\)。如果存在 \(p(x)=x\),那么说明 \((x \rightarrow x+n)\),即 \((x \rightarrow x)\),自环是不被允许的。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1000, M=6666, inf=0x3f3f3f3f;
int n, m, s, t, d[N];
int tot=1, h[N], hh[N], to[N*N], nxt[N*N], w[N*N];
int p[N], q[N];
bool v[N];
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
void add(int x,int y,int z) {
to[++tot]=y, w[tot]=z, nxt[tot]=h[x], h[x]=tot;
}
bool bfs() {
queue<int> q;
memset(d,0,sizeof(d));
d[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]||!z) continue;
d[y]=d[x]+1;
q.push(y);
if(y==t) return 1;
}
}
return 0;
}
int dfs(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]!=d[x]+1||!z) continue;
int k=dfs(y,min(res,z));
if(!k) d[y]=0; else w[i]-=k, w[i^1]+=k, res-=k;
if(k&&x!=s&&y!=t) p[x]=y-n, q[y-n]=x;
if(!res) return flow;
}
return flow-res;
}
int dinic() {
int maxflow=0;
while(bfs()) maxflow+=dfs(s,inf);
return maxflow;
}
void print(int x) {
if(!x) return;
if(q[x]!=x) print(q[x]);
v[x]=1;
printf("%d ",x);
}
int main() {
n=read(), m=read();
s=0, t=2*n+1;
for(int i=1;i<=n;++i) p[i]=q[i]=i;
for(int i=1;i<=m;++i) {
int x=read(), y=read();
add(x,y+n,1), add(y+n,x,0);
}
for(int i=1;i<=n;++i) add(s,i,1), add(i,s,0), add(i+n,t,1), add(t,i+n,0);
int ans=dinic();
for(int x=1;x<=n;++x) if(p[x]==x&&!v[x]) {
print(x), puts("");
}
printf("%d\n",n-ans);
}输出方案也可以如下(网上复制来的,不做解释)
for(int i=1;i<=n;i++){
for(int j=head[i];~j;j=e[j].next){
int v=e[j].to;
if(e[j].cap-e[j].flow==0&&e[j].flow==1){
pre[v-n]=i;
lst[i]=v-n;
}
}
}
for(int i=1;i<=n;i++){
if(!pre[i]){
int u=i;
while(lst[u]!=0){
cout<<u<<" ";
u=lst[u];
}
cout<<u<<endl;
}
}
cout<<ans<<endl;luogu2765 魔术球问题
分析
要求相邻两个数之和是完全平方数,而数据范围极小,考虑枚举。
如果将 \(x\) 在 \(y\) 上面,看作 \((y \rightarrow x)\) 的一条边,那么最终一定是一个 DAG。
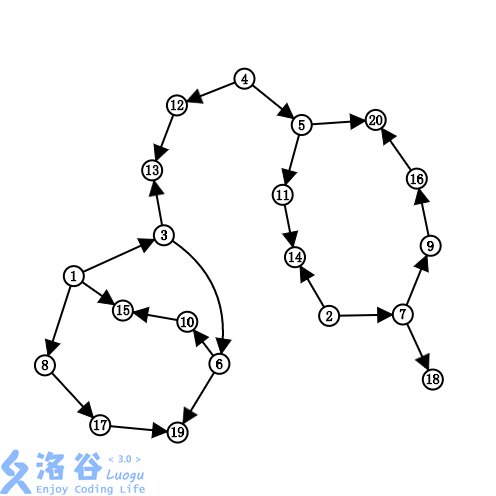
这样每个柱子实际上代表了一条路径,这些路径两两不相交,要求球数尽可能多,变相地说明对于一定量的球,路径要尽可能少。转化为 DAG 的最小路径覆盖问题。
先预处理平方。从 \(1\) 开始枚举最大编号,寻找能够放置的球的最大编号。把每个球的编号 \(x\) 拆成两个点 \(x\) 和 \(x'\),分为左部右部两个集合。
为了避免重复,规定只能从较小点连到较大点。对于一个数 \(i^2\),满足 \(i^2 > j\) 且 \(i^2 - j < j\),才连边 \((i^2 - j,j')\),容量为 \(1\)。对应 DAG 中 \((i^2 -j,j)\) 的边。
然后和源点汇点的边容量也为 \(1\),跑最大流。如果最大编号 \(T - maxflow > n\),说明需要超过 \(n\) 个柱子,此时 \(T-1\) 即为答案。
然后找最大流经过的路径就行了。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5, M=1e6+5, inf=0x3f3f3f3f;
int n, s, t, ans, d[N], squ[1145], p[N];
int tot=1, h[N], hh[N], to[M], nxt[M], w[M];
bool v[N];
void add(int x,int y,int z) {
to[++tot]=y, w[tot]=z, nxt[tot]=h[x], h[x]=tot;
}
bool bfs() {
queue<int> q;
memset(d,0,sizeof(d));
d[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]||!z) continue;
d[y]=d[x]+1;
q.push(y);
if(y==t) return 1;
}
}
return 0;
}
int dfs(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]!=d[x]+1||!z) continue;
int k=dfs(y,min(res,z));
if(!k) d[y]=0; else w[i]-=k, w[i^1]+=k, res-=k;
if(!res) return flow;
}
return flow-res;
}
int dinic() {
int maxflow=0;
while(bfs()) maxflow+=dfs(s,inf);
return maxflow;
}
int main() {
scanf("%d",&n);
s=0, t=5e4;
for(int i=1;i<=1000;++i) squ[i]=i*i;
int T=1;
while(1) {
int k=lower_bound(squ+1,squ+1000+1,T)-squ;
// 最小的大于等于T的完全平方数
add(s,T,1), add(T,s,0), add(T+1e4,t,1), add(t,T+1e4,0);
// n不是点数,不能平移n位
for(int i=1;i<=2*k;++i) {
int j=squ[i]-T;
if(j>0&&T>j) add(j,T+1e4,1), add(T+1e4,j,0);
}
ans+=dinic();
if(T-ans>n) break;
++T;
}
printf("%d\n",--T);
for(int x=1;x<=T;++x) for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(y==s||z) continue;
p[x]=y-1e4; break;
// 标记
}
for(int x=1;x<=T;++x) {
if(v[x]) continue;
for(int k=x;k;k=p[k]) {
v[k]=1;
printf("%d ",k);
}
puts("");
}
}luogu4014 分配问题
分析
跑一边最小费用最大流,再跑一边最大费用最大流。
CODE
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=105, M=4*N*N;
const ll inf=0x7fffffff;
int n, m, s, t, a[N][N], hh[N];
int tot=1, h[N], to[M], nxt[M], w[M], cst[M];
ll maxcost, mincost, d[N];
bool v[N];
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
void add(int x,int y,int z,int cost) {
to[++tot]=y, w[tot]=z, cst[tot]=cost, nxt[tot]=h[x], h[x]=tot;
}
bool SPFA1() {
queue<int> q;
for(int i=0;i<=2*n+1;++i) d[i]=inf, v[i]=0;
d[s]=0, v[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
v[x]=0;
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i], cost=cst[i];
if(!z) continue;
if(d[y]>d[x]+cost) {
d[y]=d[x]+cost;
if(!v[y]) v[y]=1, q.push(y);
}
}
}
return d[t]!=inf;
}
bool SPFA2() {
queue<int> q;
for(int i=0;i<=2*n+1;++i) d[i]=-inf, v[i]=0;
d[s]=0, v[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
v[x]=0;
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i], cost=cst[i];
if(!z) continue;
if(d[y]<d[x]+cost) {
d[y]=d[x]+cost;
if(!v[y]) v[y]=1, q.push(y);
}
}
}
return d[t]!=-inf;
}
int dfs(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
v[x]=1;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i], cost=cst[i];
if(v[y]||!z||d[y]!=d[x]+cost) continue;
int k=dfs(y,min(res,z));
w[i]-=k, w[i^1]+=k, res-=k;
if(!res) return flow;
}
v[x]=0;
return flow-res;
}
void dinic(int fg) {
while(fg? SPFA1():SPFA2()) {
memset(v,0,sizeof(v));
// mincost+=dfs(s,inf)*d[t];
fg? mincost+=dfs(s,inf)*d[t]:maxcost+=dfs(s,inf)*d[t];
}
}
void rebuild() {
memset(h,0,sizeof(h));
tot=1;
for(int i=1;i<=n;++i) {
add(s,i,1,0);
add(i,s,0,0);
add(i+n,t,1,0);
add(t,i+n,0,0);
}
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j)
add(i,j+n,1,a[i][j]), add(j+n,i,0,-a[i][j]);
}
int main() {
n=read();
s=0, t=2*n+1;
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) {
int x=a[i][j]=read();
add(i,j+n,1,x), add(j+n,i,0,-x);
}
for(int i=1;i<=n;++i) {
add(s,i,1,0);
add(i,s,0,0);
add(i+n,t,1,0);
add(t,i+n,0,0);
}
dinic(1);
printf("%lld\n",mincost);
rebuild();
dinic(0);
printf("%lld\n",maxcost);
}luogu2774 方格取数问题
分析
按照格点横纵坐标相加的奇偶性,构造二分图。由于所有格子中的数都是正数,任意两个取出的数所在的格子没有公共边,等价于先强制选择所有格子,然后删去最小的一批有冲突的格子。
最小割。
源点连向所有奇数点,容量为这个格点的数字,表示删去这个格子的代价。所有偶数点连向汇点,容量为这个格点的数字,表示删去这个格子的代价。
对于一个奇数格点,与它冲突的格点为它上下左右的偶数格点。将奇数个点与偶数个点之间连容量为 \(\infty\) 的边。表示这两个节点互斥。
在最小割中,一定不包含边权为 \(\infty\) 的边,也就是一定没有从互斥格点取数。删掉最小割之后,网络就不连通了,说明删去的都是格点,从而一定不包含所有有冲突的格点。否则由于这两个互斥的点之间的权值为 \(\infty\) 的边仍然存在,图是连通的。矛盾。
CODE
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=105, inf=0x3f3f3f3f;
const int dx[]={0, 1, 0, -1}, dy[]={1, 0, -1, 0};
int n, m, s, t, d[N*N], hh[2*N*N];
int tot=1, h[2*N*N], to[4*N*N], nxt[4*N*N], w[4*N*N];
ll sum;
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
void add(int x,int y,int z) {
to[++tot]=y, w[tot]=z, nxt[tot]=h[x], h[x]=tot;
}
bool bfs() {
queue<int> q;
memset(d,0,sizeof(d));
d[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]||!z) continue;
q.push(y);
d[y]=d[x]+1;
if(y==t) return 1;
}
}
return 0;
}
int dfs(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]!=d[x]+1||!z) continue;
int k=dfs(y,min(res,z));
if(!k) d[y]=0; else w[i]-=k, w[i^1]+=k, res-=k;
if(!res) return flow;
}
return flow-res;
}
int id(int x,int y) { return (x-1)*m+y; }
ll dinic() {
ll maxflow=0, flow=0;
while(bfs()) while(flow=dfs(s,inf)) maxflow+=flow;
return maxflow;
}
int main() {
n=read(), m=read();
s=0, t=n*m+1;
for(int i=1;i<=n;++i) for(int j=1;j<=m;++j) {
int awa=read();
sum+=awa;
if((i+j)&1) {
add(s,id(i,j),awa), add(id(i,j),s,0);
for(int k=0;k<4;++k) {
int x=i+dx[k], y=j+dy[k];
if(x>0&&x<=n&&y>0&&y<=m) add(id(i,j),id(x,y),inf), add(id(x,y),id(i,j),0);
}
} else add(id(i,j),t,awa), add(t,id(i,j),0);
}
printf("%lld\n",sum-dinic());
// 总量-最小割=最大收益
}luogu2045 方格取数加强版(K 方格取数)
分析
其实这题不属于网络流 24 题,但是也挺有启发意义的,顺带讲了吧。
看起来和上题很像,实际上很多性质都不同。比如本题中就无法直接构造出一张二分图,也不能用上题的删点方法。
当 \(k=1\) 时,那么将 \((i,j)\) 作为节点,有一个点权 \(a_{i,j}\),向 \((i+1,j)\) 和 \((i,j+1)\) 连边。答案为 \((1,1)\) 到 \((n,n)\) 的点权最长路。
当 \(k>0\) 时,一共走 \(k\) 次,那么对于节点 \((i,j)\),只有第一次走过时有收益,剩下 \(k-1\) 次收益均为 \(0\)。从 \((i,j)\) 出发,最多可以向 \((i+1,j)\) 和 \((i,j+1)\) 分别走 \(k\) 次。为了保证路径数量是 \(k\),可以把“走过的次数”看作容量,收益看作费用,这样就有了一个费用流模型的雏形。
但是,权值是点权,无法直接做。这就要使用一种名为「点转化边」的 Trick。
将 \((i,j)\) 拆成入点 \((i,j,0)\) 和出点 \((i,j,1)\),连边,入点和出点之间的权值(费用)等于原来的点权,容量为能够经过的次数。具体地,费用为 \(a_{i,j}\),容量为 \(1\);费用为 \(0\),容量为 \(k-1\)。
然后从出点 \((i,j,1)\) 向 \((i+1,j,0)\) 和 \((i,j+1,0)\) 连边,权值(费用)为 \(0\),容量为 \(k\)。
下图描述了 \((x \rightarrow y \rightarrow z)\),点权分别为 \(1\),\(2\),\(3\) 的情况。
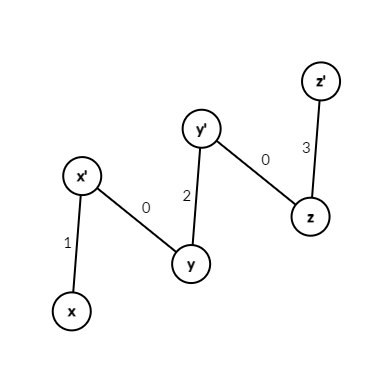
最大化权值和(总费用),最大费用最大流。
注意给节点编号,并且点转化边之后节点总量为 \(2 n^2\)。
CODE
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=5005, M=200005, inf=0x7fffffff;
int n, k, s, t, hh[N], d[N];
int tot=1, h[N], to[M], nxt[M], w[M], cst[M];
bool v[N];
int read() {
int a=0, f=1; char c=getchar();
while(!isdigit(c)) {
if(c=='-') f=-1;
c=getchar();
}
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a*f;
}
int id(int i,int j,int k) {
return (i-1)*n+j+k*n*n;
}
void add(int x,int y,int z,int cost) {
to[++tot]=y, w[tot]=z, cst[tot]=cost, nxt[tot]=h[x], h[x]=tot;
to[++tot]=x, w[tot]=0, cst[tot]=-cost, nxt[tot]=h[y], h[y]=tot;
}
bool spfa() {
queue<int> q;
for(int i=0;i<=2*n*n;++i) d[i]=-inf/2, v[i]=0;
d[s]=0, v[s]=1, q.push(s);
while(q.size()) {
int x=q.front(); q.pop();
hh[x]=h[x];
v[x]=0;
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i], cost=cst[i];
if(!z) continue;
if(d[y]<d[x]+cost) {
d[y]=d[x]+cost;
if(!v[y]) v[y]=1, q.push(y);
}
}
}
return d[t]!=-inf/2;
}
int dfs(int x,int flow) {
if(x==t||!flow) return flow;
int res=flow;
v[x]=1;
for(int& i=hh[x];i;i=nxt[i]) {
int y=to[i], z=w[i], cost=cst[i];
if(v[y]||!z||d[y]!=d[x]+cost) continue;
int k=dfs(y,min(res,z));
w[i]-=k, w[i^1]+=k, res-=k;
if(!res) return flow;
}
v[x]=0;
return flow-res;
}
ll dinic() {
ll ans=0;
while(spfa()) memset(v,0,sizeof(v)), ans+=dfs(s,inf)*d[t];
return ans;
}
int main() {
n=read(), k=read();
s=1, t=2*n*n;
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) {
int x=read();
add(id(i,j,0),id(i,j,1),1,x);
add(id(i,j,0),id(i,j,1),k-1,0);
if(i<n) add(id(i,j,1),id(i+1,j,0),k,0);
if(j<n) add(id(i,j,1),id(i,j+1,0),k,0);
}
printf("%lld\n",dinic());
}