luogu5588 小猪佩奇爬树 题解
分析
分类讨论一下。
对于颜色 \(w_i\)
若 \(w_i =0\),随便选两个点都可以,\(\frac{n (n-1)}{2}\)。
若 \(w_i = 1\),设这个点为 \(x\),那么只要两个点之间的路径经过 \(x\),就是合法的。为了不重不漏,要按照一定的顺序去计算。对于一条边 \((x \rightarrow y)\),我们先令答案累加 \(sz_x \cdot sz_y\),再将 \(sz_x\) 加上 \(sz_y\)。最后累加 \(sz_x \cdot (n-sz_x)\)。手算一下就知道是对的,可以直接处理任何一个节点的颜色数量为 1 的情况,直接查询即可。
可是对于其他情况就不是那么好处理了。不难想到对于 \(w_i >1\),由于两点间有且仅有一条简单路径,所以想要经过所有这个颜色的点,就必须保证这些点全部都在同一条链上,也就是端点数量为 2。
图中的蓝色就无法找到合法的点对,贡献为 0。
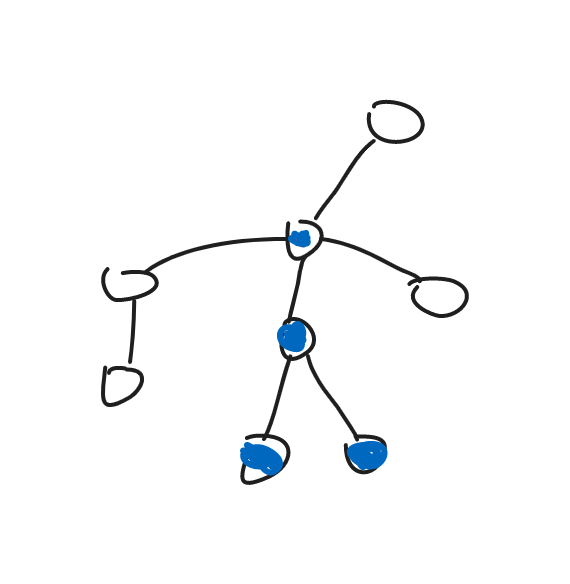
图中红色的分布就在一条链上,不难发现贡献是左端点的子树大小乘右端点子树大小。
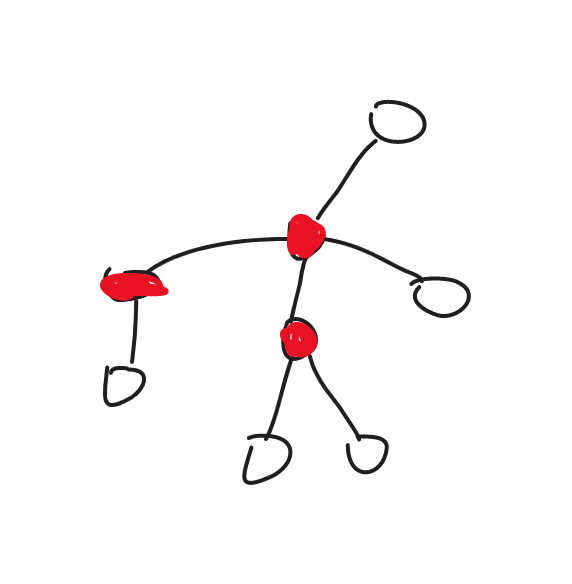
如何快速统计同一种颜色的分布情况呢?对于每种颜色单独处理是不行的。
在 dfs 的过程中,设当前节点为 \(x\),颜色为 \(c_x\),设 \(pre_{c_x}\) 为 颜色 \(c_x\) 的链上,到 \(x\) 的位置时经过的点数。用一个变量fg维护信息。(因为非链就不会产生贡献,不影响答案)
如果 \(x\) 是端点且此时 \(pre_{c_x}=0\),那么搜索完与 \(x\) 直接相连的边后最多让颜色 \(c_x\) 的点的个数 +1。相邻节点有颜色相同的,让fg+=1。
如果 \(pre_{c_x} \neq 0\) 或者不是 \(c_x\) 的最后一个节点,那么就让fg+=1,这两种情况都会让 \(x\) 可能为端点。(硬说的话前者是有机会成为后搜索到的端点,后者是有机会成为先搜索到的端点)
可以对着下面的图理解。
这样如果 \(fg=1\),那么就一定是一个端点了。
然后记录左右端点,设它们为 \((x,y)\)。
对于下图情况,直接让 \(sz_x \cdot sz_y\)
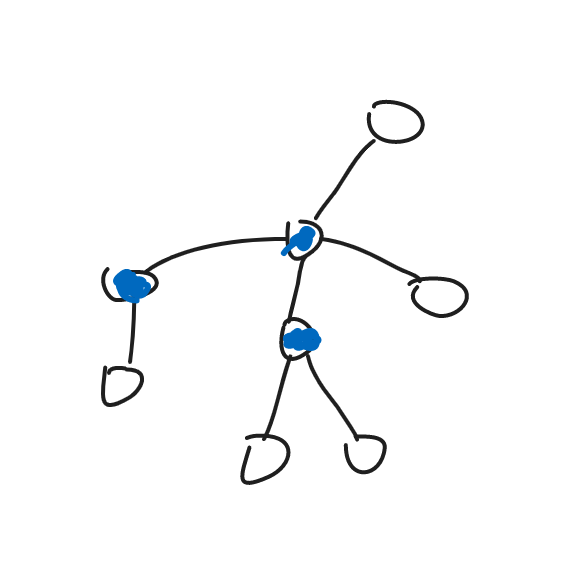
对于下图情况,设 \(dep_x>dep_y\),\(x\) 到 \(y\) 的链上第一个经过点是 \(z\),那么答案是 \(sz_y \cdot (n-sz_z)\)
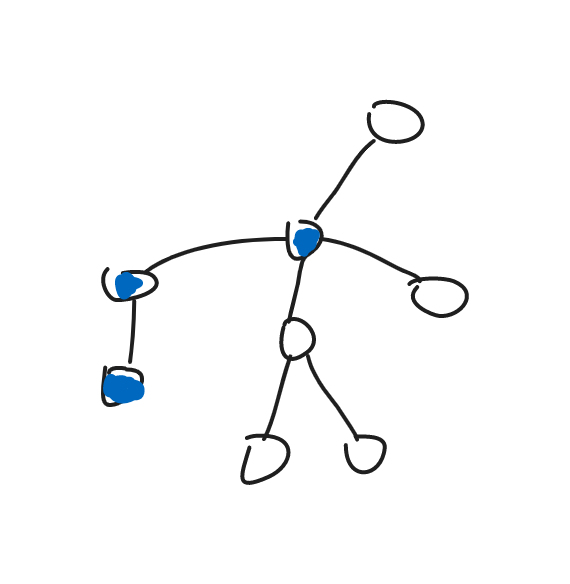
实现的时候要用好多映射,就不一一写了。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n, col[N], cnt[N], pre[N], sz[N];
long long ans1[N], ans2[N];
int cc, h[N], p[N], v[N];
struct node { int nxt, to; } e[N<<1];
void add(int x,int y) {
e[++cc]={h[x],y}, h[x]=cc;
}
// cnt[i],颜色i的总数
// col[i],i的颜色
// pre[i],颜色为i的链上已经经过的点数
void dfs(int x,int fa) {
int c=col[x], t=pre[c], fg=0, z=0;
sz[x]=1;
for(int i=h[x];i;i=e[i].nxt) {
int y=e[i].to;
if(y==fa) continue;
int lst=pre[c];
// 这里没有算上x
dfs(y,x);
ans1[x]+=1ll*sz[x]*sz[y];
sz[x]+=sz[y];
if(lst!=pre[c]) ++fg, z=y;
// 搜到了相同的颜色,记录z
}
ans1[x]+=1ll*sz[x]*(n-sz[x]);
if(t||pre[c]+1!=cnt[c]) ++fg;
++pre[c]; // x也在pre[c]的链上
if(fg==1) {
if(!v[c]) p[c]=x;
else {
int s=z? n-sz[z]:sz[x];
// n-sz[z]的情况实际是搜索到的第一个这个颜色的节点就是端点
ans2[c]=1ll*sz[p[c]]*s;
}
++v[c]; // 端点数量
}
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;++i) {
scanf("%d",&col[i]);
++cnt[col[i]], p[col[i]]=i;
}
for(int i=1;i<n;++i) {
int x, y; scanf("%d%d",&x,&y);
add(x,y), add(y,x);
}
dfs(1,0);
for(int i=1;i<=n;++i) {
if(!cnt[i]) printf("%lld\n",1ll*n*(n-1)/2);
else if(cnt[i]==1) printf("%lld\n",ans1[p[i]]);
// 注意i是颜色,要用p[i]映射过去
else if(v[i]==2) printf("%lld\n",ans2[i]);
// 有两个端点
else puts("0");
}
}