luogu2294 狡猾的商人 题解
solution1 带权并查集
给出的信息是区间和的形式,搞个前缀和数组 \(a_i\),表示 \([1,i]\) 月的总收益。
假如知道 \([x,y]\) 月的收益与 \([y,z]\) 月的收益,那么就能推出 \([x,z]\) 月的收益。这时候如果后来的 \([x,z]\) 月的信息产生冲突,那么必定是假的。
由于不同区间的信息具有可合并性和传递性,考虑带权并查集。
首先明确 \(a_i\) 此时表示 \([fa(i),i]\) 的和。这是带权并查集的固定套路。
当给出一个区间信息 \((u,v,w)\) 表示 \([u,v]\) 这一段的和为 \(w\) 时,找到 \(x=fa(u-1)\),\(y=fa(v)\)。
如果 \(x \neq y\),那么令 \(fa(y)=x\),也就是将这两段区间合并。关键在于如果处理合并后区间的和。
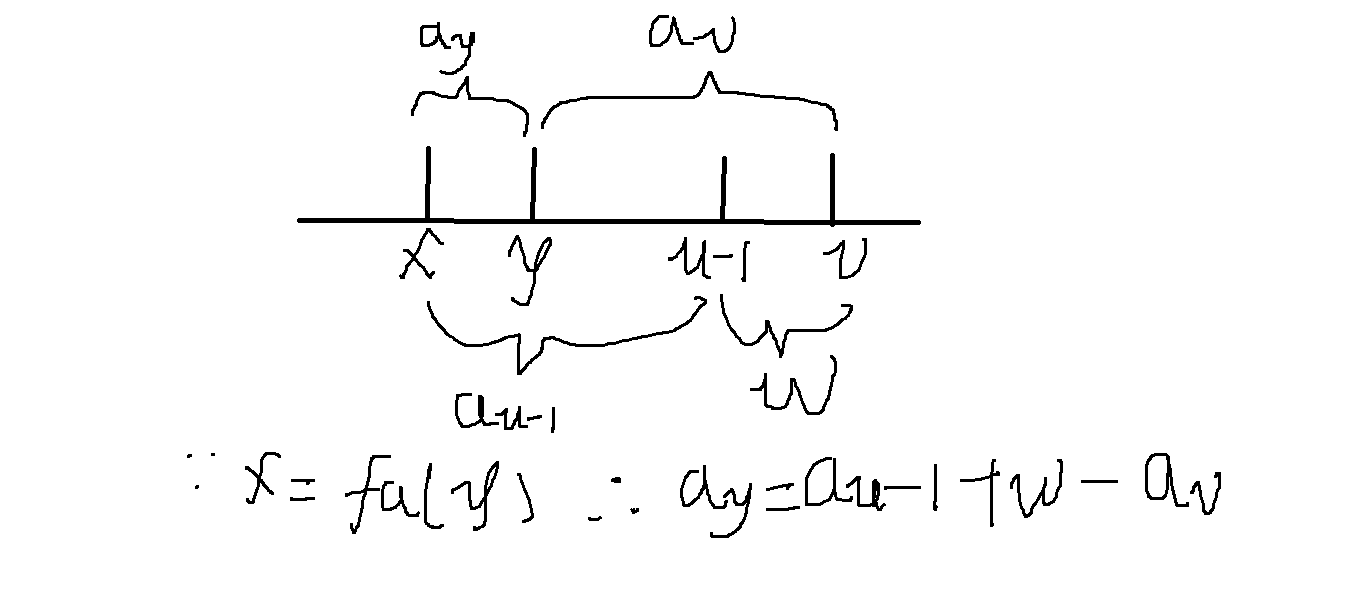
很明确了。更新 \(a_y = a_{u-1}+w-a_v\)。
如果上图中 \(x\) 在 \(y\) 的右边也没有问题,只不过 \(a_y\) 是个负数,理论上也是讲得通的。
如果 \(x=y\),那么直接判断 \(a_v - a_{u-1}\) 是否等于 \(w\)。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=105, M=5005;
int T, n, m;
namespace union_set {
int a[N], f[N];
int get(int x) {
if(x==f[x]) return x;
int t=get(f[x]);
a[x]+=a[f[x]];
// 路径压缩必定要做的事
return f[x]=t;
}
void solve() {
n=read(), m=read();
for(int i=0;i<=n;++i) f[i]=i, a[i]=0;
bool fg=1;
while(m--) {
int u=read(), v=read(), w=read();
int x=get(u-1), y=get(v);
if(x==y) {
if(a[v]-a[u-1]!=w) fg=0;
}
else f[y]=x, a[y]=a[u-1]-a[y]+w;
}
puts(fg? "true":"false");
}
};solution2 差分约束系统
这个更显然了。但是给出了是 \([u,v]\) 区间和一定是 \(w\)。那么直接转化 \(X_v - X_{u-1} = z\),\(X_{u-1} - X_v = -z\)。由于是直接等于,那么直接添加双向边add(u-1,v,z)和add(v,u-1,-z)。
SPFA 跑最短路,判负环。
图不一定连通,那就搞一个超级源点 \(n+1\),对于节点 \(i \in [0,n+1]\),连接add(n+1,i,0)。注意 \(u-1\) 能取到 0,所以不能用 0 当超级源点。
有负环说明账本是假的。
CODE
namespace cfys {
const int inf=0x3f3f3f3f;
int dep[N], d[N], v[N];
int cnt, h[N], to[M], nxt[M], w[M];
queue<int> q;
void add(int x,int y,int z) { to[++cnt]=y, w[cnt]=z, nxt[cnt]=h[x], h[x]=cnt; }
bool SPFA() {
while(q.size()) q.pop();
for(int i=0;i<=n+1;++i) d[i]=inf, v[i]=0, dep[i]=0;
d[n+1]=0, q.push(n+1), v[n+1]=1;
while(q.size()) {
int x=q.front(); q.pop();
v[x]=0;
for(int i=h[x];i;i=nxt[i]) {
int y=to[i], z=w[i];
if(d[y]>d[x]+z) {
d[y]=d[x]+z;
if(++dep[y]>n+1) return 0;
// 0到n一共n+1个节点
// 最短路长度超过n+1说明存在负环
if(!v[y]) v[y]=1, q.push(y);
}
}
}
return 1;
}
void solve() {
cnt=0;
memset(h,0,sizeof(h));
n=read(), m=read();
while(m--) {
int x=read(), y=read(), z=read();
add(x-1,y,z), add(y,x-1,-z);
}
for(int i=0;i<=n;++i) add(n+1,i,0);
puts(SPFA()? "true":"false");
}
};luogu2294 狡猾的商人 题解
https://yozora0908.github.io/2022/lg2294-solution/