二分图匹配简单题 题解
写一下近期写的简单二分图题目的题解。
luogu3967 匹配
分析
\(TJOI\) 板子题 \(\times 1\)。
找出所有完美匹配的交集,意思是无论任何完美匹配都包含这些边,反过来,如果没有这些边中任意一边,都不存在完美匹配。
由于数据范围小,直接用 DFS 版的 \(KM\) 算法求出带权最大匹配。然后枚举每一条匹配边, 把它的边权置为 \(0\),表示删去它。如果此时求出的带权最大匹配小于之前求出的带权最大匹配,那么这条边就是必须包含的边。
CODE
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=150, inf=1<<30;
int n, dlt, match[N], t[N], w[N][N], la[N], lb[N], slack[N];
ll Ans;
bool va[N], vb[N];
struct node { int x, y; } p[N];
bool operator<(node a,node b) { return a.x<b.x; }
bool dfs(int x) {
va[x]=1;
for(int y=1;y<=n;++y) if(!vb[y]) {
if(la[x]+lb[y]==w[x][y]) {
vb[y]=1;
if(!match[y]||dfs(match[y])) {
match[y]=x; return 1;
}
} else slack[y]=min(slack[y],la[x]+lb[y]-w[x][y]);
}
return 0;
}
ll KM() {
for(int i=0;i<=n;++i) {
la[i]=-inf, lb[i]=0;
match[i]=0;
for(int j=1;j<=n;++j) la[i]=max(la[i],w[i][j]);
}
for(int i=1;i<=n;++i) while(1) {
memset(va,0,sizeof(va)), memset(vb,0,sizeof(vb));
for(int j=1;j<=n;++j) slack[j]=inf;
if(dfs(i)) break;
dlt=inf;
for(int j=1;j<=n;++j) if(!vb[j]) dlt=min(dlt,slack[j]);
for(int j=1;j<=n;++j) {
if(va[j]) la[j]-=dlt;
if(vb[j]) lb[j]+=dlt;
}
}
ll ans=0;
for(int i=1;i<=n;++i) ans+=la[i]+lb[i];
return ans;
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) scanf("%d",&w[i][j]);
printf("%lld\n",Ans=KM());
for(int i=1;i<=n;++i) t[i]=match[i];
// match在之后的KM算法中要被修改,所以记录原来的匹配边,
int tot=0;
for(int i=1;i<=n;++i) {
int x=t[i], y=i, d=w[x][y];
w[x][y]=0;
if(KM()<Ans) {
p[++tot].x=x, p[tot].y=y;
}
w[x][y]=d;
}
sort(p+1,p+tot+1);
// 要求排序再输出
for(int i=1;i<=tot;++i) printf("%d %d\n",p[i].x,p[i].y);
}luogu4304 攻击装置
分析
\(TJOI\) 板子题 \(\times 2\)。这个貌似和网络流 24 题中的骑士共存问题很想,不是那么板,但是只要会跑最大匹配就能过。
首先观察这个东西的攻击范围,不难发现,对于 \((x,y)\),它能够攻击的点的横纵坐标相加一定与 \(x+y\) 异奇偶。于是乎直接将横纵坐标相加为奇数的看作左部点,偶数的为右部点。为了防止重复计数,钦定如果 \((x,y)\) 为左部点且能够放置,那么由它向能够攻击到的右部点连边。
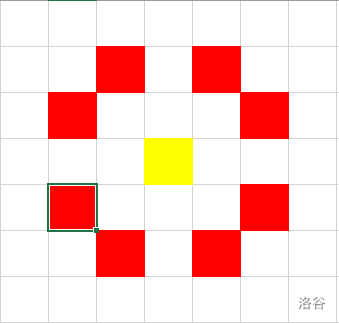
由于放置的装置不能互相攻击,等价于选出这张二分图的最大独立集。用能够放置的点数减去最大匹配的边数即可。
CODE
#include<bits/stdc++.h>
using namespace std;
const int T=205, N=400005;
const int dx[8]={-1,-2,1,2,-1,-2,1,2}, dy[8]={-2,-1,-2,-1,2,1,2,1};
int n, m, times, a[T][T], g[T][T], v[N];
int tot, match[N], h[N], to[8*N], nxt[8*N];
// 8倍空间
void add(int x,int y) { to[++tot]=y, nxt[tot]=h[x], h[x]=tot; }
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
bool dfs(int x) {
for(int i=h[x];i;i=nxt[i]) {
int y=to[i];
if(v[y]==times) continue;
v[y]=times;
if(!match[y]||dfs(match[y])) return match[y]=x;
}
return 0;
}
int xiongyali() {
int res=0;
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) if((i+j)&1&&g[i][j]) {
// 从左部点 DFS
++times;
res+=dfs(g[i][j]);
}
return res;
}
int main() {
n=read();
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) {
scanf("%1d",&a[i][j]);
if(!a[i][j]) g[i][j]=++m;
}
for(int i=1;i<=n;++i) for(int j=1;j<=n;++j)
if(g[i][j]&&(i+j)&1) for(int k=0;k<8;++k) {
// 放置重复,只从左部点开始连边
int x=i+dx[k], y=j+dy[k];
if(x>0&&y>0&&x<=n&&y<=n&&g[x][y]) add(g[i][j],g[x][y]);
}
printf("%d\n",m-xiongyali());
}luogu3033 Cow Steeplechase
分析
首先两条线段如果平行,那么必定没有交点。那么把竖着的线段作为左部点,横着的线段作为右部点。那么同一个点集内没有边,左部点 \(i\) 与右部点 \(j\) 最多有一条匹配边,符合二分图匹配模型。
钦定 \(x_{i,1} \le x_{i,2}\),\(y_{i,1} \le y_{i,2}\)。
对于线段 \((x_{i,1},y_{i,1})\),\((x_{i,2},y_{i,2})\) 和 \((x_{j,1},y_{j,1})\),\((x_{j,2},y_{j,2})\),它们相交的条件是
- \(i\) 是竖着的边,\(j\) 是横着的边。那么要满足 \(x_{i,1} \ge x_{j,1}\) 且 \(y_{i,1} \le y_{j,1}\) 且 \(x_{i,2} \le x_{j,2}\) 且 \(y_{i,2} \ge y_{j,2}\)。
- \(i\) 是横着的边,\(j\) 是竖着的边。那么就把上面的符号反过来。
选出最多的不相交线段,等价于二分图最大独立集。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n, m, x1[N], y11[N], x2[N], y2[N];
int tot, match[N], h[N], to[N], nxt[N];
bool l[N], v[N];
void add(int x,int y) { to[++tot]=y, nxt[tot]=h[x], h[x]=tot; }
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
bool dfs(int x) {
for(int i=h[x];i;i=nxt[i]) {
int y=to[i];
if(v[y]) continue;
v[y]=1;
if(!match[y]||dfs(match[y])) return match[y]=x;
}
return 0;
}
int xiongyali() {
int res=0;
for(int i=1;i<=n;++i) if(l[i]) {
memset(v,0,sizeof(v));
res+=dfs(i);
}
return res;
}
int main() {
n=read();
for(int i=1;i<=n;++i) {
x1[i]=read(), y11[i]=read();
x2[i]=read(), y2[i]=read();
if(x1[i]>x2[i]) swap(x1[i],x2[i]);
if(y11[i]>y2[i]) swap(y11[i],y2[i]);
if(x1[i]==x2[i]) ++m, l[i]=1;
// m是左部点数量,也就是竖着的边
}
for(int i=1;i<n;++i) for(int j=i+1;j<=n;++j) {
if(l[i]&&!l[j]) {
if(x1[i]>=x1[j]&&y11[i]<=y11[j]&&x2[i]<=x2[j]&&y2[i]>=y2[j])
add(i,j+m);
} else if(!l[i]&&l[j]) {
if(x1[i]<=x1[j]&&y11[i]>=y11[j]&&x2[i]>=x2[j]&&y2[i]<=y2[j])
add(j,i+m);
}
}
printf("%d\n",n-xiongyali());
}luogu4589 智力竞赛
分析
\(TJOI\) 板子题 \(\times 3\)。
首先明确,每个人答题顺序一定是一条简单路径,可以有人答相同的题目。而且所有题目构成一个 DAG。
好了,DAG 最小路径可重复点覆盖。
二分答案,找到一个 \(mid\) 表示只能回答价值小于 \(mid\) 的问题。如果求得的路径条数小于 \(n+1\)(亲友团加上小明),那么说明可行。特别的,如果回答所有问题也能满足条件的话,输出AK。
CODE
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=505, inf=0x3f3f3f3f;
int n, m, T, a[N][N], d[N], match[N], v[N], vis[N];
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
bool dfs(int x) {
for(int y=1;y<=m;++y) if(vis[y]!=T&&a[d[x]][d[y]]) {
vis[y]=T;
if(!match[y]||dfs(match[y])) return match[y]=x;
}
return 0;
}
bool check(int x) {
int cnt=0;
for(int i=0;i<=m;++i) match[i]=d[i]=0;
for(int i=1;i<=m;++i) if(v[i]<x) d[++cnt]=i;
int ans=cnt;
for(int i=1;i<=cnt;++i) {
++T; ans-=dfs(i);
}
return ans<=n+1;
}
int main() {
int l=0, r=0;
n=read(), m=read();
for(int i=1;i<=m;++i) {
r=max(r,v[i]=read()); int k=read();
while(k--) {
int x=read();
a[i][x]=1;
}
}
for(int k=1;k<=m;++k)
for(int i=1;i<=m;++i)
for(int j=1;j<=m;++j)
a[i][j]|=a[i][k]&a[k][j];
if(check(inf)) { puts("AK"); return 0; }
while(l<r) {
int mid=(l+r+1)/2;
if(check(mid)) l=mid; else r=mid-1;
}
printf("%d\n",l);
}