「Edu Codeforces Round」#133 (Div 2)

CF1716.

A. 2-3 Moves

分析

注意到 \(n=1\) 的时候要使用 \(+3\)，\(-2\) 两次操作。

如果 \(3 \mid n\)，那么全部用 \(3\) 就好，操作数 \(\frac{n}{3}\)。

否则当 \(n \equiv 2 \pmod 3\) 时，先用一次 \(2\) 然后全部用 \(3\) 即可，操作数 \(\lfloor \frac{n}{3} \rfloor + 1\)。

否则一定有 \(n \equiv 1 \pmod 3\)，那么由于 \(n \neq 1\)，所以必定存在一个 \(4\)，用两次 \(2\)，剩下的一定是 \(3\) 的倍数。不难发现操作数仍然是 \(\lfloor \frac{n}{3} \rfloor + 1\)。

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+5;
int t, n, ans;
int read() {
	int a=0, f=1; char c=getchar();
	while(!isdigit(c)) {
		if(c=='-') f=-1;
		c=getchar();
	}
	while(isdigit(c)) a=a*10+c-'0', c=getchar();
	return a*f;
}
void solve() {
	n=read();
	if(n==1) ans=2;
	else if(n%3==0) ans=n/3;
	else ans=n/3+1;
	printf("%lld\n",ans);
}
signed main() {
	t=read();
	while(t--) solve();
}

B. Permutation Chain

分析

注意最优解中第一次肯定是从 \(1\) 到 \(n\)，fixedness 为 \(n\)。经过一次交换后 fixedness 必定为 \(n-2\)，之后每一次交换都一定有办法让 fixedness 减少 \(1\)，最终为 \(0\)。

直接输出 \(n\) 然后随便乱搞即可。

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=105;
int t, n, ans[N];
int read() {
	int a=0, f=1; char c=getchar();
	while(!isdigit(c)) {
		if(c=='-') f=-1;
		c=getchar();
	}
	while(isdigit(c)) a=a*10+c-'0', c=getchar();
	return a*f;
}
void print(int* a) {
	for(int i=1;i<=n;++i) printf("%lld%c",a[i]," \n"[i==n]);
}
void solve() {
	n=read();
	printf("%lld\n",n);
	int p=1;
	for(int i=1;i<=n;++i) ans[i]=i;
	print(ans);
	for(int i=n-2;~i;--i) {
		swap(ans[p],ans[p+1]);
		print(ans);
		++p;
	}
}
signed main() {
	t=read();
	while(t--) solve();
}

C. Robot in a Hallway

分析

由于本人比较懒，所以直接用网图了 awa。侵删。

由于要经过每一个格子，所以走法必定是先走蛇形然后「コ」形。~~实在是无法形容所以直接用这个片假名 orz~~。当然也可以全部走蛇形或者全部走「コ」形，其中蛇形必然是先向下走。

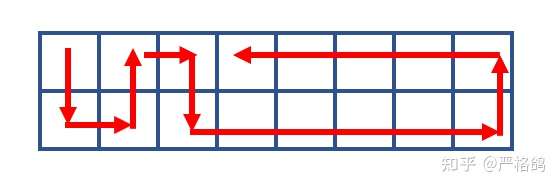
这张图也就说明了「コ」形路线必然确定了终点的位置。

设 \(f(i=0/1,j)\) 为从起点到达 \((i,j)\)，再向右走「コ」形最终到达 \((i \operatorname{xor} 1,j)\) 的时间。转移如下

能到达 \((i,j)\) 的最早时间为 \(a_{i,j} + 1\)，如果路上所有格子都能够经过，那么走到 \((i \operatorname{xor} 1,j)\) 的最早时间为还要加上 \(2 \cdot (n-j+1) -1\)。
\(f(i,j+1)\) 差一步就走到 \((i \operatorname{xor} 1,j)\) 了，如果此时 \((i \operatorname{xor} 1,j)\) 可以经过，时间就要加上 \(1\)。
\(a_{i \operatorname{xor} 1,j} + 1\)，题目规定的最早时间。

三种情况取最大值。

但是此时最小的 \(f(i,j)\) 仍然不一定是答案。就比如

3
0 5 1
5 1 1

手算易得答案为 \(10\)，但是最小的 \(f(i,j)\) 答案为 \(3\)。

这是因为我们默认了从起点到 \((i,j)\) 的过程中畅通无阻。此时只要设当前时间为 \(cur\)，假设后面所有点都畅通无阻就行了，时间为 \(cur + 2 \cdot (n-j+1) -1\)。

那么下面这组数据呢？

4
0 5 1 100
5 1 1 100

上面的那种解决方案失效了，可是又被 \(f(i,j)\) 的第二种转移覆盖了。

模拟走蛇形路线，计算将每个 \(i\) 作为终点的时间即可。

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+5;
int t, n, a[2][N], f[2][N];
int read() {
	int a=0, f=1; char c=getchar();
	while(!isdigit(c)) {
		if(c=='-') f=-1;
		c=getchar();
	}
	while(isdigit(c)) a=a*10+c-'0', c=getchar();
	return a*f;
}
void solve() {
	n=read();
	for(int i=0;i<=1;++i) for(int j=1;j<=n;++j) a[i][j]=read();
	a[0][1]=-1;
	f[0][n+1]=f[1][n+1]=0;
	for(int i=0;i<=1;++i) for(int j=n;j;--j) {
		f[i][j]=max(max(a[i][j]+1+2*(n-j+1)-1,f[i][j+1]+1),a[i^1][j]+1);
	}
	int cur=0, ans=1ll<<60;
	for(int j=1;j<=n;++j) {
		int i=(j-1)&1;
		ans=min(ans,max(f[i][j],cur+2*(n-j+1)-1));
		cur=max(cur,a[i][j]+1)+1;
		cur=max(cur,a[i^1][j]+1)+1;
	}
	printf("%lld\n",ans);
}
signed main() {
	t=read();
	while(t--) solve();
}

这不比 D 难？

D. Chip Move

分析

问题转化一下。有一个 \(0 \rightarrow n\) 的数轴，从 \(0\) 开始跳跃任意次，第 \(i\) 次跳跃的距离是 \(k+i-1\) 的倍数。

对于 \(x \in [1,n]\)，求出跳到 \(x\) 的方案数。

设 \(\Delta_i = k+i-1\)，\(f(j)\) 为跳到 \(j\) 的方案数。注意到将 \(i\) 作为阶段的话，计算 \(f\) 的过程相当于完全背包问题。背包容量为 \(j\)，物品体积则为 \(\Delta_i\)，选择 \(\Delta_i\) 的 \(n\) 倍就是 \(n\) 个 \(\Delta_i\)。

对于每个阶段，分别累加答案即可。

注意完全背包问题是每个物品可以选择任意次，但是本题至少选择 \(1\) 次。所以可以使用「平移」的办法，令 \(i\) 阶段的 \(f(j)\) 的值等于 \(i-1\) 阶段 \(f(j-\Delta_i)\) 的值，这样就相当于强制选择一个 \(\Delta_i\)。

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+5, mod=998244353;
int t, n, k, f[N], ans[N];
int read() {
	int a=0, f=1; char c=getchar();
	while(!isdigit(c)) {
		if(c=='-') f=-1;
		c=getchar();
	}
	while(isdigit(c)) a=a*10+c-'0', c=getchar();
	return a*f;
}
void solve() {
	n=read(), k=read();
	for(int i=0;i<=n;++i) ans[i]=0;
	f[0]=1;
	int cur=0;
	for(int i=1;i<=n;++i) {
		int dlt=k+i-1;
		cur+=dlt;
		for(int j=n;j>=dlt;--j) f[j]=f[j-dlt];
		for(int j=0;j<dlt;++j) f[j]=0;
		for(int j=dlt;j<=n;++j) (f[j]+=f[j-dlt])%=mod;
		for(int j=dlt;j<=n;++j) (ans[j]+=f[j])%=mod;
		if(cur>n) break;
	}
	for(int i=1;i<=n;++i) printf("%lld%c",ans[i]," \n"[i==n]);
}
signed main() {
	solve();
}