分析

放一张题面里的图。

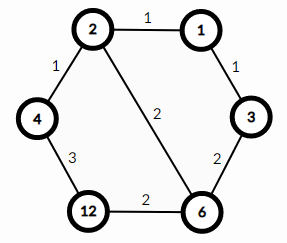
能发现走一条边就是除掉或加入一个质因子。

从 \(x\) 走到 \(y\) 的最短路，一定是先除掉若干质因子，再加入若干质因子。中间那个临界点是 \(d=\gcd(x,y)\)。

然后考虑一条节点不断变小的路径，发现它的边权和可以消去中间项，只和首位有关。因此 \((x \rightarrow d)\) 与 \((y \rightarrow d)\) 的最短路和具体消去质因子的顺序无关。

以 \((x \rightarrow d)\) 为例。把 \(\frac{x}{d}\) 分解为 \(\prod_{i=1}^m p_i^{e_i}\)，则消去质因子的方案数是 \[ f\Big(\frac{x}{d}\Big) = \frac{(\sum_{i=1}^m e_i)!}{\prod_{i=1}^m(e_i!)} \] 最终答案就是 \(f\Big(\frac{x}{d}\Big) \times f\Big(\frac{y}{d}\Big)\)。

CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
int read() {
	int a=0, f=1; char c=getchar();
	while(!isdigit(c)) {
		if(c=='-') f=-1;
		c=getchar();
	}
	while(isdigit(c)) a=a*10+c-'0', c=getchar();
	return a*f;
}
const int mod=998244353;
int D, q, cnt, d[100], fac[100];
// 虽然D很大，但是质因数个数和质因数指数都是log级别的
int fp(int a,int b) {
	int c=1;
	for(;b;a=a*a%mod,b>>=1) if(b&1) c=c*a%mod;
	return c;
}
int calc(int x) {
	int p=0, q=1;
	for(int i=1;i<=cnt;++i) if(x%d[i]==0) {
		int e=0;
		while(x%d[i]==0) x/=d[i], ++e;
		p+=e, (q*=fac[e])%=mod;
	}
	return fac[p]*fp(q,mod-2)%mod;
}
int gcd(int x,int y) { return y? gcd(y,x%y):x; }
signed main() {
	D=read(), q=read();
	for(int i=2;i*i<=D;++i) if(D%i==0) {
		while(D%i==0) D/=i;
		d[++cnt]=i;
	}
	if(D>1) d[++cnt]=D;
	fac[0]=fac[1]=1;
	for(int i=2;i<=100;++i) fac[i]=fac[i-1]*i%mod;
	while(q--) {
		int x=read(), y=read();
		int z=gcd(x,y);
		printf("%lld\n",calc(x/z)*calc(y/z)%mod);
	}
}