CF1338B Edge Weight Assignment 题解
分析
没错还是构造……
明确某个数异或另一个数偶数次,结果仍然是它本身。
再明确所有的数字都是正整数,不能用 \(0\)。
任意两个叶子之间的路径权值的异或和为 \(0\),如果它们之间的距离是偶数的话,那么都填同一个数就好了。最小数量为 \(1\)。
如果存在某两个叶子之间的距离不为偶数,如下图 \(1\) 和 \(5\)。
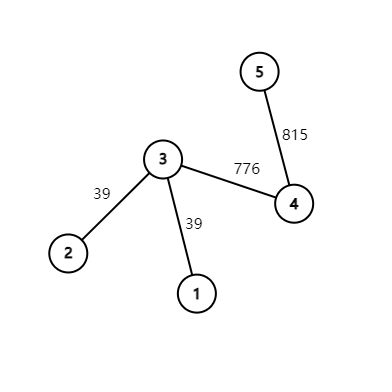
钦定 \((1 \rightarrow 3)\) 的权值为 \(39\),那么如果 \((3 \rightarrow 4)\) 或者 \((4 \rightarrow 5)\) 任何一个是 \(39\),\(39 \operatorname{xor} 39 =0\),结果都是另一条边的权值。所以假如 \((4 \rightarrow 5)\) 是 \(815\),那么 \((3 \rightarrow 4)\) 只有是 \(39 \operatorname{xor} 815=776\) 才能满足异或和为 \(0\)。
其实这就相当于把两条边「合并」为一条边,权值为它们的异或值,这样奇数距离就转化成了偶数。至于更长的奇数距离的情况,依旧这样去做,不难发现这种情况下最少使用 \(3\) 种权值。
那么最多呢?直接做不好想,考虑从它的补集入手。如果没有任何限制,那么一定是每一条边一个权值,共有 \((n-1)\) 种。然后再减去会「因为某些边权的确定而被动确定的边」就行了。
依旧是上图,假如上述权值不变,那么 \((2 \rightarrow 3)\) 能够填什么呢?\((1 \rightarrow 5)\) 和 \((2 \rightarrow 5)\),在 \((3 \rightarrow 5)\) 这一段是重叠的,只有 \((2 \rightarrow 3)\) 的权值与 \((1 \rightarrow 3)\) 相同,才能让异或和为 \(0\)。不难发现,对于同一个父亲的叶子节点,它们与父亲之间的边只能是一种。假如一个点 \(x\) 有 \(t_x\) 个叶子节点,其中 \(t_x-1\) 条边的权值一定是与剩下那一条相同的。
综上所述,权值最多的情况,就是 \[ n-1 - \sum_{x \in V \text{ and } t_x \ge 1} t_x -1 \] 注意如果 \(t_x=1\),贡献是 \(0\),如果 \(t_x=0\) 也没有贡献。
因为是无根树,所以要钦定根节点。
对于寻找最小数量,可以找到一个叶子节点作为根,判断它到其他叶子节点的距离是否都是偶数,是的话答案为 \(1\),否则为 \(3\)。因为树的奇妙性质所以不会存在某个叶子和另一个叶子到「根」的距离是偶数,但是它们之间的距离是奇数的问题。
在寻找最大值时,如果还从叶子节点开始搜索的话会产生遗漏,所以从以一个非叶子节点为根,统计 \(t_x\)。
CODE
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n, sum;
int tot, h[N], to[N<<1], nxt[N<<1];
bool flag=1;
void add(int x,int y) { to[++tot]=y, nxt[tot]=h[x], h[x]=tot; }
int read() {
int a=0; char c=getchar();
while(!isdigit(c)) c=getchar();
while(isdigit(c)) a=a*10+c-'0', c=getchar();
return a;
}
void dfs1(int x,int fa,int dis) {
if(!nxt[h[x]]&&dis&1) flag=0;
// 与某个叶子节点距离为奇数
for(int i=h[x];i;i=nxt[i]) {
int y=to[i];
if(y==fa) continue;
dfs1(y,x,dis+1);
}
}
void dfs2(int x,int fa) {
int t=0;
for(int i=h[x];i;i=nxt[i]) {
int y=to[i];
if(y==fa) continue;
dfs2(y,x);
t+=!nxt[h[y]];
// !nxt[h[y]]=1,叶子
}
if(t) sum+=t-1;
}
int main() {
n=read();
if(n==2) { puts("1 1"); return 0; }
for(int i=1;i<n;++i) {
int x=read(), y=read();
add(x,y), add(y,x);
}
int root=0;
for(int i=1;!root&&i<=n;++i) if(!nxt[h[i]]) root=i;
// 叶子节点
dfs1(root,0,0);
root=0;
for(int i=1;!root&&i<=n;++i) if(nxt[h[i]]) root=i;
// 非叶子节点
dfs2(root,0);
printf("%d %d\n",flag? 1:3,n-sum-1);
}