分析

首先转化一下题意。

对于一个 \(n \times m\) 的格子图，每个格子都有一个初始权值 \(a_{i,j}\)，有两种操作：

1. 将两个相邻格子的权值都 +1
2. 将一个格子的权值 +2

求能将所有格子的权值变为相同且满足每个权值都在 \([L,R]\) 范围内的初始局面的个数。

这种题目可以从奇偶性下手。

对于操作 1，实质是同时改变两个相邻格子的奇偶性。

对于操作 2，实质是在不改变该格子的奇偶性的前提下增大或减小权值。

那么只要我们让所有格子权值的奇偶性相同就行了。

设奇数个数为 \(A\)，偶数个数为 \(B\)。那么有 \(n \times m = A + B\)。

考虑操作 1，如果那两个格子都是奇数，那么 \(A+2\)，如果一奇一偶，那么 \(A\) 不变，如果都为偶数，那么 \(A-2\)。也就是说，无论怎样改变使用操作 1，都不会改变 \(A\) 的奇偶性，同时 \(A\) 与 \(B\) 此消彼长，\(B\) 的奇偶性也不会变化。

由于最终一定会让 \(A\) 与 \(B\) 的其中一个变成 0，所以 \(A\) 与 \(B\) 中至少有一个是偶数，否则无解。

但是似乎题目保证有解。

先说一下，向下图这样，将两个格子所在的路径上所有的格子都进行操作 1，最终就会单独改变这两个格子的奇偶性。

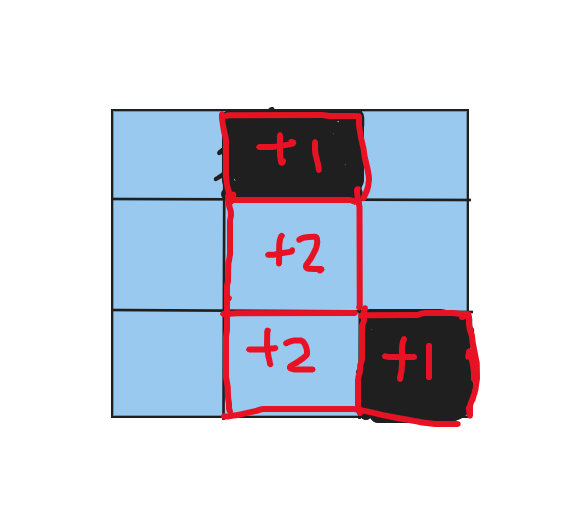
因此只要 \(A\) 与 \(B\) 其中一个是偶数，就有解。

如何计数呢？再分成两种情况讨论。

1. \(A\) 与 \(B\) 一奇一偶

由于 \(n \times m = A + B\)，那么 \(n \times m\) 是奇数，从而 \(n\) 与 \(m\) 都是奇数。

在这种情况下，要么 \(A\) 是奇数，要么 \(B\) 是奇数。所以无论图中初始权值是多少，都一定能满足上述条件，随便选就行。

由于每个格子的取值都在 \([L,R]\) 中，所以答案为 \((R-L+1)^{n \times m}\)

2. \(A\) 与 \(B\) 都是偶数

不难得到 \(n \times m\) 是偶数。

由于要保证 \(A\) 是偶数，所以答案是 \[ \sum_{2 \mid A}^{nm} C_{nm} ^A \cdot k^A \cdot l^B \] 其中 \(k\) 是 \([L,R]\) 中的奇数个数，\(l\) 为 \([L,R]\) 中的偶数个数。

然而这个式子是没法求的，根本找不到 \(A\) 与 \(B\)。

考虑二项式定理 \[ (k+l)^{nm} = \sum_{a=0}^{nm} C_{nm}^a \cdot k^a \cdot l^{nm-a} \]

\[ (k-l)^{nm} = \sum_{a=0}^{nm} (-1)^{a} C_{nm}^a \cdot k^a \cdot l^{nm-a} \]

由于 \(B = n \times m - A\)，所以将两式相加，\(a\) 是奇数时相抵消，\(a\) 是偶数时算了两遍，最终答案是 \[ \frac{(k+l)^{nm} + (k-l)^{nm}}{2} \]

CODE

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll p=998244353;
ll n, m, L, R;
ll fp(ll x,ll y) {
	ll z=1;
	for(;y;x=x*x%p,y>>=1) if(y&1) z=z*x%p;
	return z;
}
int main() {
	scanf("%lld%lld%lld%lld",&n,&m,&L,&R);
	ll w=R-L+1;
	if((n&1)&&(m&1)) printf("%lld\n",fp(w,n*m));
	else {
		ll k=R/2-(L-1)/2;
		ll l=w-k;
		printf("%lld\n",(fp((k+l)%p,n*m)+fp(k-l+p,n*m))*499122177%p);
        // 499122177是2在模998244353意义下的逆元
	}
}