考虑 DP。

DP 需要一定的顺序。因为给出的矩形没有包含的关系，所以我们按照每个矩形右上角点的横坐标 \(x\) 递增排序，那么纵坐标 $ y$ 一定是递减排序的。

设 \(S_i = x_i \times y_i\)。

因为每个矩形都有选与不选两种选择，所以设 $ f(i)$ 为在排序后的 \([1,i]\) 中，必须选择第 \(i\) 个矩形获得的最大收益，也就是选出的矩形面积之并减去代价。

初始值为 \(f(i) = S_i-a_i\)。

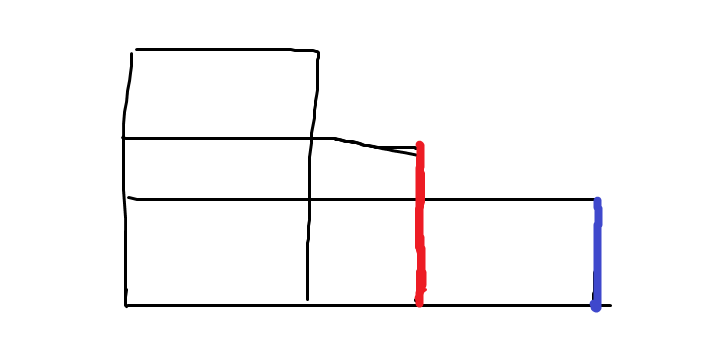
因为状态中只限制了选择第 \(i\) 个，而矩形的选择是没有限制的。所以转移时找到 \(j \in [1,i)\)，用选择 \(j\) 的最大收益 \(f(j)\) 选择 \(i\) 的初始收益并且减去二者之交。或者说是 \(f(j)\) 加上 \(S_i \cup S_j\) 减去代价。 \[ f(i)=\max_{j \in [1,i)}{ \{ f(j)+ S_i - a_i - S_i \cap S_j \} } \] 有一个问题是，难道 \(i\) 不会和之前选择的一些矩形有重叠部分吗？在下图中，设宽为黑色的是 \(k\)，红色的是 \(j\)，蓝色的是 \(i\)，满足 \(k < j < i\)。那么计算 \(f(j)\) 的时候必然已经减去了 \(S_j \cap S_k\)，得到了 \(S_j \cup S_k\)。排序后，\(S_i \cap S_j\) 一定包含了 \(S_i \cap S_k\)，也就是 \(S_i \cap S_j = S_i \cap (S_j \cup S_k)\)，从而 \(S_i\) 与 \(f(j)\) 中选出的矩形面积之并就等于 \(f(j)+S_i - S_i \cap S_j\)。也就是不会出现这种问题。

答案为

\[ \max_{1 \le i \le n}\{ f(i) \} \]

复杂度为 $ O(n^2)$。

复杂度过高，考虑优化。

由于我们已经将矩形排序，所以

\[ \forall j \le i \quad x_i \ge x_j,y_i \le y_j \]

即

\[ S_i \cup S_j = x_j \times y_i \]

所以原方程可化简为 \[ f(i) = \max_{ 1 \le j < i } { \{ f(j)+ x_iy_i - a_i -x_jy_i \} } \] 按照套路去掉 \(\large \max\) 函数，移项得 \[ f(j)=y_ix_j +f(i) - x_iy_i + a_i \] 即

\[ \begin{cases} y=f(j) \\ k=y_i \\ x=x_j \\ b= f(i)-x_iy_i+a_i \end{cases} \]

对应到坐标系里即为：

每个决策点为 $ (x_j,f(j))$，其斜率 $ y_i$ 单调递减，所以要维护一个上凸壳。

由于斜率 \(y_i\) 单调递减 ，所以合法决策的斜率一定小于 \(y_i\)。

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
#define ll long long
#define X(y) (w[y].x)
#define Y(x) (f[x])
const int N=1e6+6;
ll n, ans, q[N], f[N];
struct Squ { ll x, y, z; } w[N];
bool operator<(Squ a,Squ b) { return a.y>b.y; }
double calc(ll x,ll y) { return X(x)!=X(y)? 1.0*(Y(x)-Y(y))/(X(x)-X(y)):1e9; }
int main() {
    int i;
    scanf("%lld",&n);
    for(i=1;i<=n;++i) scanf("%lld%lld%lld",&w[i].x,&w[i].y,&w[i].z);
    sort(w+1,w+n+1);
    int l=1, r=1;
    for(i=1;i<=n;++i) {
        f[i]=w[i].x*w[i].y-w[i].z;
        while(l<r&&calc(q[l],q[l+1])>=w[i].y) ++l;
        f[i]=max(f[i],f[q[l]]+(w[i].x-w[q[l]].x)*w[i].y-w[i].z);
        ans=max(ans,f[i]);
        while(l<r&&calc(q[r-1],q[r])<=calc(q[r],i)) --r;
        q[++r]=i;
    }
    printf("%lld\n",ans);
}